Plots not rendering properly on an implicit plot (python)-CodePudding

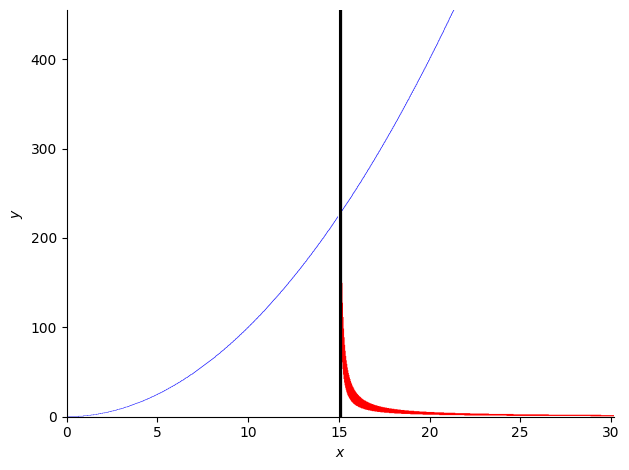
I am trying to plot two curves and then mark their intersection with a vertical line from the x-axis to the point of intersection.

Sometimes the line will generate other times it will not unless I show the plot and then append it as well. To see this try option 1 with b = 24, c = 159 then try option 4 where a = 15, c = -19. Below is the code, any help would be great, thanks!

import math
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import sys
from sympy import *
from sympy.plotting import plot, plot_implicit, plot_parametric
from sympy import sympify

def find_intersection(F,G):
    result = sym.solve([F,G],(x,y))
    return result

def check_roots(roots):
    i=0
    complexsol = 0
    negativesol = 0
    while i < 3:
        rx, ry = roots[i]
        if sympify(rx).is_real == True:
            if rx > 0:
                return rx, ry
                break
            else:
                print('Root ', i 1 ,  ' was discarded for being negative')
                negativesol = negativesol   1
        else:
            print('Root ', i 1,  ' was discarded for being complex')
            complexsol = complexsol   1 
        i =1  
    if negativesol   complexsol == 3:
        sys.exit("There are no solutions by Khayyam's method")

def plot_solution(F, G, xroot, yroot):
    newxroot = float(xroot)
    newyroot = float(yroot)
    x, y = symbols('x y')
    plot1 = plot_implicit(F, (x,0,2*newxroot), (y,0,2*newyroot), line_color='b',show=False)
    plot2 = plot_implicit(G, (x,0,2*newxroot), (y,0,2*newyroot), line_color='r',show=False)
    plot1.append(plot2[0])
    plot3 = plot_implicit(Eq(x, newxroot),(x,0,newxroot), (y,0,newyroot), line_color='black', show=False)
    plot1.append(plot3[0])
    plot1.show()
    print('Approximate x1 solution is: ', round(newxroot,1))
    print('Exact x1 solution is: ', newxroot)


print('Solving cubics using two conic sections in the sytle of Omar Khayyam')
print('Cubic forms:')
print('0: Cancel program')
print('1: x^3   bx = c')
print('2: x^3   ax^2   bx   c = 0')
print('3: x^3   c = bx')
print('4: x^3   c = ax^2')
print('5: x^3   ax^2 = c')
print('6: x^3 = bx   c')
print('7: x^3 = ax^2   c')

userchoice = input('Please choose the form of your cubic or press 0 to cancel: ')

if userchoice == '0':
    sys.exit('You have chosen to cancel the program')
  
if userchoice == '1':
    # good choice is 15, -14
    b = int(input('Enter your b value: '))
    c = int(input('Enter your c value: '))

    x, y = sym.symbols('x y')
    eq1 = sym.Eq(x**2/math.sqrt(b),y)
    eq2 = sym.Eq(b*x**2   b*y**2, c*x)
    
    exact_sols = find_intersection(eq1,eq2)
    xsol, ysol = check_roots(exact_sols)
    plot_solution(eq1, eq2, xsol, ysol)

if userchoice == '2':
    # good choice is -6,11,-6
    a = int(input('Enter your a value: '))
    b = int(input('Enter your b value: '))
    c = int(input('Enter your c value: '))

    x, y = sym.symbols('x y')
    eq1 = sym.Eq(x**2,y)
    eq2 = sym.Eq((x   a)*(y   b), a*b-c)
    
    exact_sols = find_intersection(eq1,eq2)
    xsol, ysol = check_roots(exact_sols)
    plot_solution(eq1, eq2, xsol, ysol)

if userchoice == '3':
    # good choice is 15, -14
    b = int(input('Enter your b value: '))
    c = int(input('Enter your c value: '))

    x, y = sym.symbols('x y')
    eq1 = sym.Eq(x**2,y)
    eq2 = sym.Eq(x*y   c, b*x)
    
    exact_sols = find_intersection(eq1,eq2)
    xsol, ysol = check_roots(exact_sols)
    plot_solution(eq1, eq2, xsol, ysol)

if userchoice == '4':
    # good choice is 15,-14
    a = int(input('Enter your a value: '))
    c = int(input('Enter your c value: '))

    x, y = sym.symbols('x y')
    eq1 = sym.Eq(x**2,y)
    eq2 = sym.Eq(x*y   c, a*y)
    
    exact_sols = find_intersection(eq1,eq2)
    xsol, ysol = check_roots(exact_sols)
    plot_solution(eq1, eq2, xsol, ysol)

if userchoice == '5':
    # good choice is 15, -14
    a = int(input('Enter your a value: '))
    c = int(input('Enter your c value: '))

    x, y = sym.symbols('x y')
    eq1 = sym.Eq(x**2,y)
    eq2 = sym.Eq(x*y   a*y, c)
    
    exact_sols = find_intersection(eq1,eq2)
    xsol, ysol = check_roots(exact_sols)
    plot_solution(eq1, eq2, xsol, ysol)
    
if userchoice == '6':
    # good choice is 15, -14
    b = int(input('Enter your b value: '))
    c = int(input('Enter your c value: '))

    x, y = sym.symbols('x y')
    eq1 = sym.Eq(x**2,y)
    eq2 = sym.Eq(x*y, b*x   c)
    
    exact_sols = find_intersection(eq1,eq2)
    xsol, ysol = check_roots(exact_sols)
    plot_solution(eq1, eq2, xsol, ysol)
    
if userchoice == '7':
    # good choice is 15, 19
    a = int(input('Enter your a value: '))
    c = int(input('Enter your c value: '))

    x, y = sym.symbols('x y')
    eq1 = sym.Eq(x**2,y)
    eq2 = sym.Eq(x*y, a*y   c)
    
    exact_sols = find_intersection(eq1,eq2)
    xsol, ysol = check_roots(exact_sols)
    plot_solution(eq1, eq2, xsol, ysol)

Sometimes it worked if i redered plot3 (the intersection line) before plot2 (one of the curves) but this was not always a successful solution.

PS if it also finds that there are no positive roots it exits the programme and should display a message (line 32), which it does but it also displays an error message saying 'An exception has occurred, use %tb to see the full traceback.' if anyone knows how to fix this that would also be helpful!

CodePudding user response：

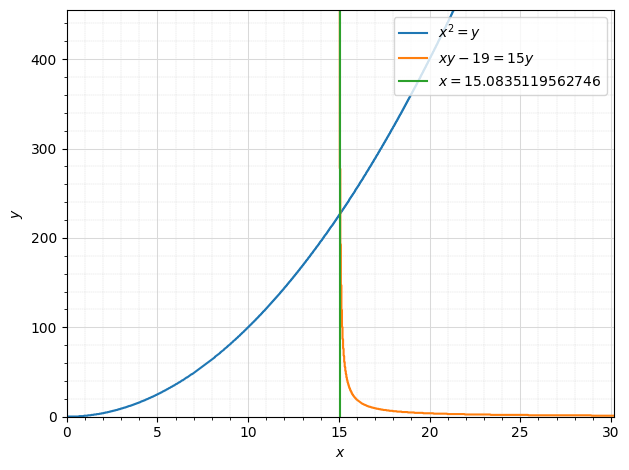
Replace the plot3 = plot_implic.... command with the following:

plot3 = plot_implicit(Eq(x, newxroot),(x,0,2*newxroot), (y,0,2*newyroot), line_color='black', show=False, adaptive=False)

Note that I used adaptive=False which should create a constant width line, and I also plotted the vertical line over the same range as the two previous expressions.

Also, I suggest using an

Note the constant-width lines and labels.