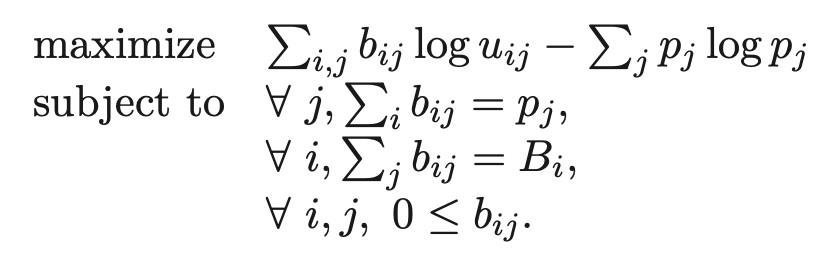CVXR incorrectly claiming problem is infeasible?-CodePudding

I want to solve the following convex optimization problem, where b is a matrix of variables and p is a vector of variables. The matrix u is a matrix of fixed non-negative values.

Here is my formulation in R, using the CVXR package. When I run it, SCS tells me that the status is unbounded. Am I formulating the problem incorrectly, or is this a bug in CVXR? Mathematically, it's easy to see that the objective function is bounded from above, so the problem cannot be unbounded.

R code

library(CVXR)

assemble_problem <- function(u, B) {
    # Get size of problem, number of goods and bidders
    m = nrow(u)  # bidders
    n = ncol(u)  # goods
    
    # Define variables
    b <- Variable(m, n, name="spending", nonneg=TRUE)
    p <- Variable(n, name="prices")
    
    # Assemble objective
    logu = apply(u, 1:2, log)  # apply the log function to each entry in u
    objective <- Maximize(sum(b*logu)   sum(entr(p)))
    
    # Assemble constraints
    constraints <- list()
    # Budget constraints
    for (i in 1:m) { append(constraints, list(sum(b[i,]) == B[i])) }
    # Spending constraints
    for (j in 1:n) { append(constraints, list(sum(b[,j]) == p[j])) }
        
    # Create and return problem
    problem <- Problem(objective, constraints)
    return(problem)
}


# Example
u <- matrix(c(1, 2, 3, 4), 2, 2)
B <- c(1, 1)
problem <- assemble_problem(u, B)
solution <- solve(problem, solver = "SCS", FEASTOL = 1e-4, RELTOL = 1e-3, verbose = TRUE)
# solution$status

Julia code

For completeness, I'm also attaching a Julia formulation (using Convex.jl) of the problem, which manages to solve the problem correctly.

using Convex, SCS

function assemble_problem(u, B)
    # Get size of problem, number of bidders m and goods n
    m, n = size(u)

    # Define variables
    b = Variable(m, n, Positive())
    p = Variable(n)

    # Assemble objective
    logu = log.(u)
    objective = sum(logu .* b)   entropy(p)
    
    # Assemble constraints
    constraints = Constraint[]
    # Budget constraints
    for i in 1:m push!(constraints, sum(b[i,:]) == B[i]) end
    # Price constraints
    for j in 1:n push!(constraints, sum(b[:,j]) == p[j]) end

    # Initialise and return problem
    problem = maximize(objective, constraints)
    return b, p, problem
end

u = [1 3; 2 4]
B = [1, 1]
b, p, prog = assemble_problem(u, B)
solve!(prog, () -> SCS.Optimizer())

CodePudding user response：

append in R does not work like push! in Julia. You have to assign the output:

  # Budget constraints
  for (i in 1:m) { constraints <- append(constraints, list(sum(b[i,]) == B[i])) }
  # Spending constraints
  for (j in 1:n) { constraints <- append(constraints, list(sum(b[,j]) == p[j])) }

Your list of constraints is empty otherwise.