I'm trying to write a Python function which does the following:

1. Takes in an array of points where each point has:
   • Position from 0 to 1 (x)
   • Weight (w)
2. Smoothly interpolates between them in such a way that point weights are taken into account.

To make it more clear, here's an illustration:

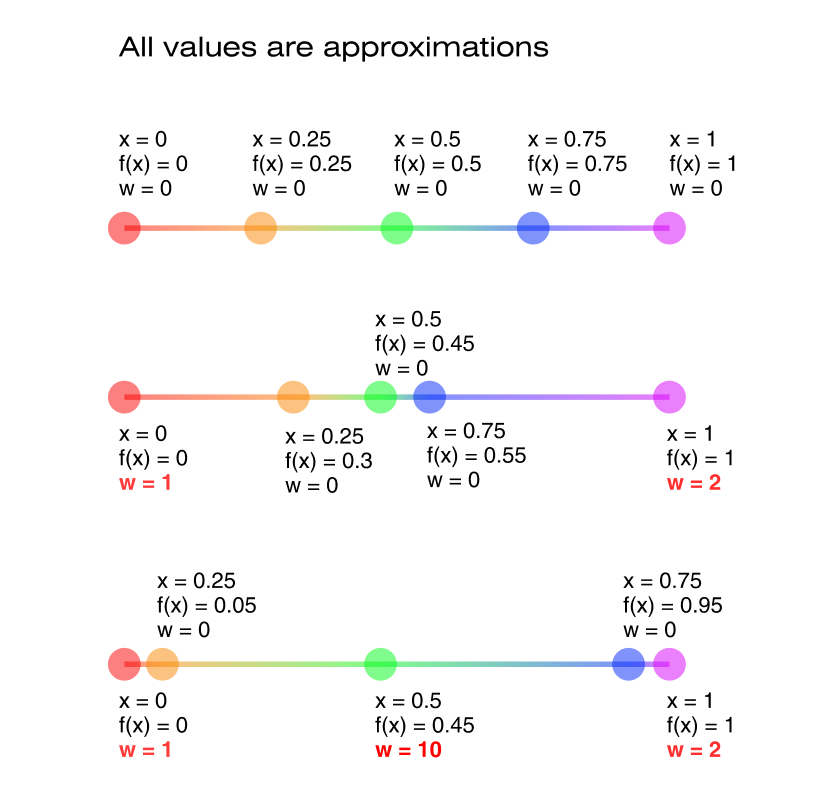
Notice how points with weights are "pushing" other points around.

CodePudding user response：

One possibility is to make up a rule, for instance:

The distance between two adjacent points should be proportional to the sum of their weights.

This rule does not seem perfectly consistent with your examples. In your examples, it looks like every point repulses every other point, not just adjacent points.

But it has the advantage of being a simple rule.

Here is an implementation of this rule in python:

from itertools import pairwise, accumulate

def place_points(weights):
    if all(w == 0 for w in weights):
        return [p / (len(weights)-1) for p in range(0, len(weights))]
    else:
        dists = [w1 w2 for w1,w2 in pairwise(weights)]
        positions = list(accumulate(dists, initial=0))
        total_dist = positions[-1]
        normalised_positions = [p / total_dist for p in positions]
        return normalised_positions

for weights in ([0,0,0,0,0], [1,0,0,0,2], [1,0,10,0,2]):
    print('weights: ', weights)
    print('points:  ', place_points(weights))
    print()

# weights:  [0, 0, 0, 0, 0]
# points:   [0.0, 0.25, 0.5, 0.75, 1.0]

# weights:  [1, 0, 0, 0, 2]
# points:   [0.0, 0.333, 0.333, 0.333, 1.0]

# weights:  [1, 0, 10, 0, 2]
# points:   [0.0, 0.043, 0.478, 0.913, 1.0]

CodePudding user response：

Here is a physics model that slowly moves the points around as if they were sliding magnets.

At each iteration, the force exerted on each magnet is calculated, and the magnet moves accordingly.

The repulsion exerted by a magnet over another magnet is proportional to the inverse of the square of the distance between the two, because that's how it works for actual magnets.

import numpy as np
#import matplotlib.pyplot as plt  ## uncomment those lines for graphics output

def move_points(weights, points=None, left=0, right=1, n_iter = 1000, learning_rate = 0.0001):
    n = weights.shape[0]
    if not points:
        points = np.linspace(0, 1, n)
    assert(points.shape == weights.shape == (n,))
    #plt.scatter(points, [0]*n)
    for t in range(1, n_iter 1):
        dists = (points - points.reshape((n,1)))
        coeffs = np.sign(dists) / dists**2
        forces = np.nansum(weights*coeffs, axis=1)
        points = points - learning_rate * forces
        points[0] = max(left, points[0])
        points[-1] = min(points[-1], right)
        #plt.scatter(points, [t]*n)
    #plt.show()
    return points

Testing:

for weights in map(np.array, ([0,0,0,0,0], [1,0,0,0,2], [1,0,10,0,2])):
    print('weights: ', weights)
    print('points:  ', move_points(weights, n_iter=100))
    print()

# weights:  [0 0 0 0 0]
# points:   [0.   0.25 0.5  0.75 1.  ]

# weights:  [1 0 0 0 2]
# points:   [0.         0.32732937 0.46804381 0.59336546 1.        ]

# weights:  [ 1  0 10  0  2]
# points:   [0.         0.11141358 0.46804381 0.83729092 1.        ]

Graphics output of trajectories:

Weights = [0 0 0 0 0]

Weights = [1 0 0 0 2]

Weights = [1 0 10 0 2]