Plot `semilogx` graph for Euclidean distances matrix-CodePudding

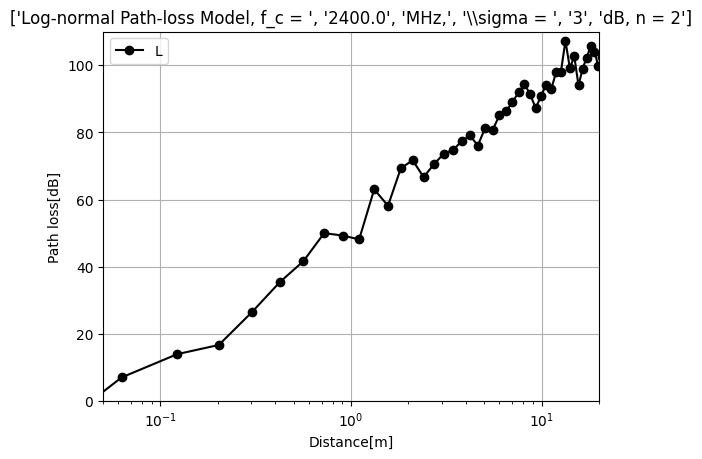
I am struggling to make a semilogx plot for the Euclidean distances matrix. I want a single line to show the differences, but the Euclidean distances matrix lists different items.

When making the plot using the distance = np.arange(0.05, 15, 0.1) ** 2, the line appears as expected.

However, when I use the following code blocks that generate the Euclidean distances matrix, it no longer appears in a single line.

m = random((8, 2))
distance_matrix = cdist(m, m)

What's the best way to plot the Euclidean distances matrix based on the following code I have done so far?

from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
import numpy as np

# % Log-distance or Log-normal shadowing path loss model
# % Inputs: fc : Carrier frequency[Hz]
# % d : Distance between base station and mobile station[m]
# % d0 : Reference distance[m]
# % n : Path loss exponent
# % sigma : Variance[dB]
def logdist_or_norm(fc, d, d0, n, sigma):
    lamda = 3e8 / fc
    PL = -20 * np.log10(lamda / (4 * np.pi * d0))   10 * n * np.log10(d / d0)
    
    if sigma:
        # PL = PL   sigma * np.random.randn(d.shape)
        PL = PL   sigma * np.random.randn(len(d))
    return PL

# % Channel Parameters
fc = 2.4e9 #% operation in 2.4 GHz
d0 = 0.25  #% good choice for inddor distances (microcells)
sigma = 3  #% keep the book suggestion
Gt = 1     #% No transmitter antenna gain as provided by nordic datasheet 
Gr = 1     #% No receiver antenna gain as provided by nordic datasheet 
Exp = 4;    #% Mid value in the obstructed in building range (Table 1.1)
# Exp = 1    #% Mid value in the obstructed in building range (Table 1.1)

# % Distance vector also for plot
# distance = np.arange(0.05, 15, 0.1) ** 2
m = np.random.random((8, 2))
distance = cdist(m, m)

# np.random.randn(len(distance))

# % Log-normal shadowing model
y_lognorm = logdist_or_norm(fc, distance.flatten(), d0, Exp, sigma)

# % Plot Path loss versus distance
plt.semilogx(distance.flatten(), y_lognorm, 'k-o')
plt.grid(True), plt.axis([0.05, 20, 0, 110]), plt.legend('Log-normal shadowing model')
plt.title(['Log-normal Path-loss Model, f_c = ', str(fc/1e6),'MHz,', '\sigma = ', str(sigma), 'dB, n = 2'])
plt.xlabel('Distance[m]'), plt.ylabel('Path loss[dB]')

Expectation

CodePudding user response：

Sort the x values and remove the zeroes before calculating the y values; don't add noise; return both x and y values.

def logdist_or_norm(fc, d, d0, n, sigma):
    d.sort()
    (d,) = d.nonzero()
    lamda = 3e8 / fc
    PL = -20 * np.log10(lamda / (4 * np.pi * d0))   10 * n * np.log10(d / d0)
    
    if sigma:
        pass
        # PL = PL   sigma * np.random.randn(d.shape)
        # PL = PL   sigma * np.random.randn(len(d))
    return d,PL

...
...
# % Log-normal shadowing model
distance,y_lognorm = logdist_or_norm(fc, distance.flatten(), d0, Exp, sigma)
...
...