I have a graph that is not binary, and is of single direction. It can look like the following:

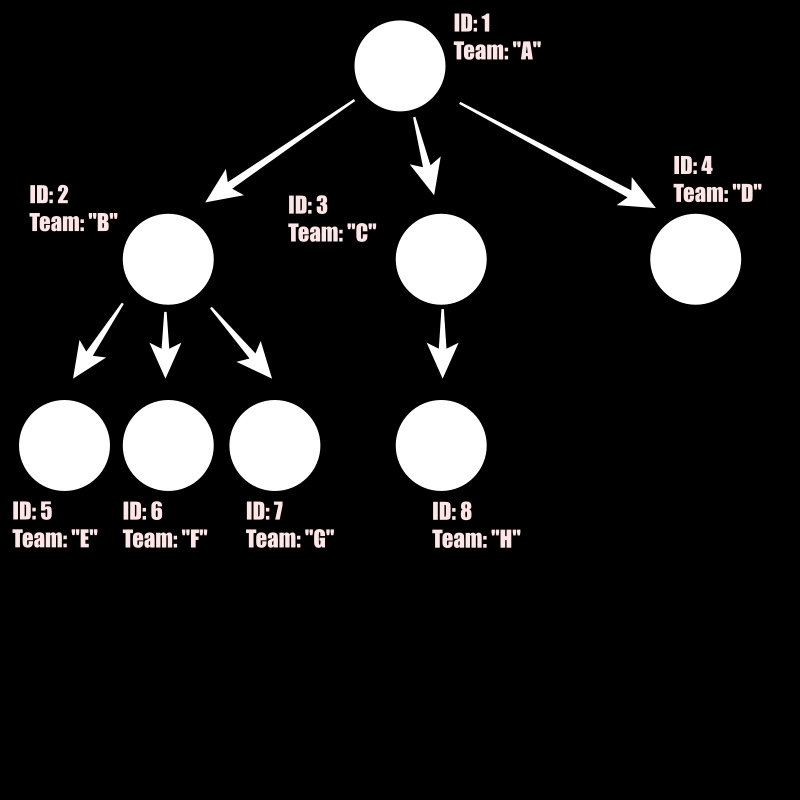
I would like to find the shortest path, for example Team "G" to Team "D". What methods can I use?

CodePudding user response：

By "of single direction" I imagine what you mean is that the tree is represented by nodes which only point at the children, not at the parents. Given that, user3386109's comment provides a simple way to get the answer you are looking for.

1. Find the path from the root to the first node by doing any tree traversal, like in-order (even if the order of children is insignificant, in practice, there will be some way to enumerate them in some order), and record the sequence of nodes from the root to the first node. In your example, we would get G-B-A (assuming a recursive solution where we are printing these nodes in reverse order).

2. Find the path from the root to the second node in the same way. Here, we'd get a path like D-A.

3. Find the first common ancestor of the two nodes; assuming the nodes are labeled uniquely as in this example, we can simply find the first symbol in either string of nodes, that is also in the other string of nodes. Regardless of which string we start with, we should get the same answer, as we do in your example: A

4. Chop off everything in both strings after the common ancestor, reverse one of the strings, and concatenate them with the common ancestor in the middle. This gives a path starting with node1 going to node2. Note that the problem asks for the shortest path; however, in a tree, there will be exactly one path between any two nodes. In your example, we get G-B-A-D.

Some pseudocode...

class Node {
    char label;
    Node[] children;
}

string FindPath(Node root, Node node1, Node node2) {
    // make sure we have valid inputs
    if (root == null || node1 == null || node2 == null) return null;

    // look for paths to the nodes from the root
    string path1 = FindPath(root, node1);
    string path2 = FindPath(root, node2);

    // one of the nodes wasn't found
    if (path1 == null || path2 == null) return null;

    // look for first common node
    // note: this isn't the most efficient approach, see
    // comments on time complexity below
    for (int i = 0; i < path1.Length; i  ) {
        char label = path1[i];
        if (path2.Contains(label) {
            path1 = path1.Substring(0, i);
            path2 = path2.Substring(0, path2.IndexOf(label);
            return path1   label   ReverseString(path2);
        }
    }

    // will never reach here because it's guaranteed we will find
    // a common ancestor in a tree
    throw new Exception("Unreachable statement");
}

string FindPath(Node root, Node node) {
    // make sure inputs are valid
    if (root == null || node == null) return null;

    if (root.label == node.label) {
        // found the node
        return node.label;
    } else {
        // this is not the node, exit early if no children
        if (root.children == null || root.children.Count == 0) return null;

        // check each child and if we find a path, return it
        foreach (Node child in root.children) {
            string path = FindPath(child, node);
            if (path != null && path.Length > 0) {
                return path   root.label;
            }
        }

        // it's possible that the target node is not in this subtree
        return null;
    }
}

In terms of the number of nodes in the tree, the complexity should look like...

1. Getting the path from the root to each node should at worst visit each node in the tree, so O(|V|)
2. Looking for the first common node... well, a naive approach would be O(|V|^2) if we use the code as proposed above, since in the worst case, the tree is split in two long branches. But, we could be a little smarter and start at the end and work our way back as long as the strings match, and return the last matching node we saw as soon as we see that they don't match anymore (or we run out of symbols to check). Coding that is left as an exercise and that should be O(|V|)