Tuning the percentiles of a probability density function with values of mu and sigma-CodePudding

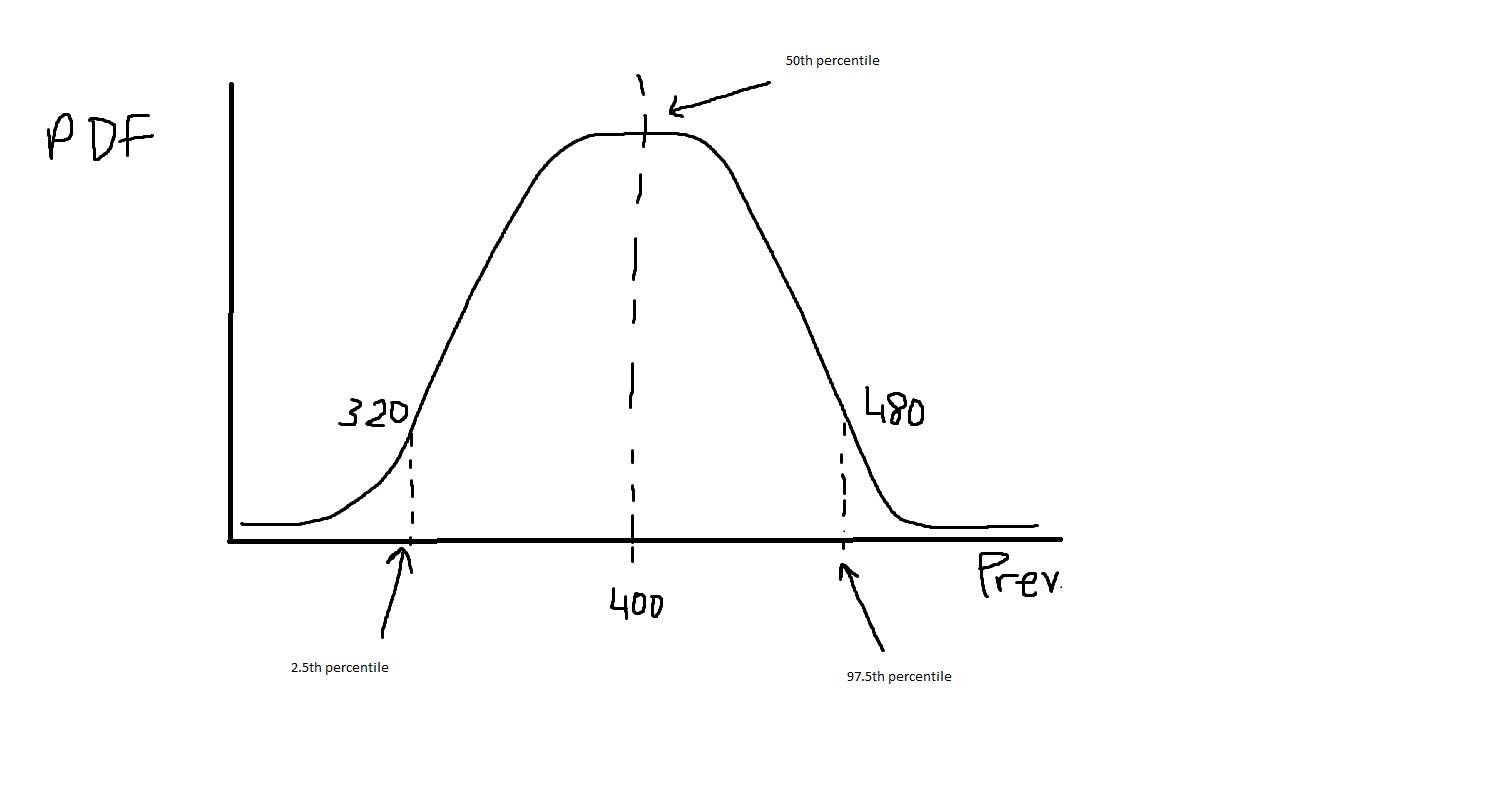
I am trying to probability density functions something like the sketch below:

so that the 50th percentile of the distribution has the highest PDF value, and it is at 400. Then the 2.5th and 97.5th percentiles are 320 and 480 respectively. Here is my code I tried:

import numpy as np

mu, sigma = 3, 1. # mean and standard deviation
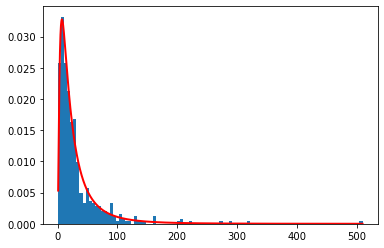
s = np.random.lognormal(mu, sigma, 480)
import matplotlib.pyplot as plt
count, bins, ignored = plt.hist(s, 100, density=True, align='mid')
x = np.linspace(min(bins), max(bins), 10000)
pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
       / (x * sigma * np.sqrt(2 * np.pi)))
plt.plot(x, pdf, linewidth=2, color='r')
plt.axis('tight')
plt.show()

The issues I am having is defining the range for the function I want. By placing 480 in the line s = np.random.lognormal(mu, sigma, 480) does not change the shape of the distribution. Secondly, by change the values of mu and sigma, it merely changes the scale on the x axis. Where is my methodology going wrong?

CodePudding user response：

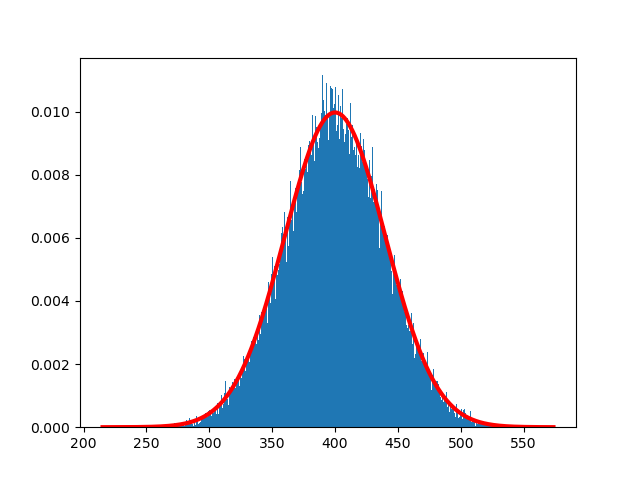
I might misunderstand the question, but in case you are looking for a normal distribution with a mean of 400 and standard deviation of 40, you could use this:

mu, sigma = 400, 40.
s = np.random.normal(mu, sigma, 100000)
count, bins, ignored = plt.hist(s, 1000, density=True)
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
           np.exp( - (bins - mu)**2 / (2 * sigma**2) ),linewidth=3, color='r')