I’m familiar with the Hamilton path for a directed graph - visit every node exactly once.
I’m looking for an algorithm to walk the graph so that I visit every node at least once. I can’t find the standard name for this problem, if any.
This graph is walkable - root-a-d-b-c
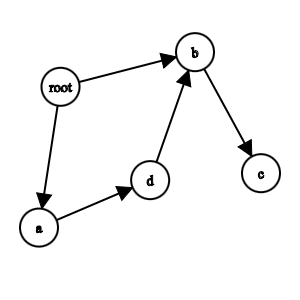
This graph is not walkable - because in my walk, if I reach c, I have no directed edge to reach a & d and conversely, if I walk to a, d; there’s no directed edge that takes me to b & c
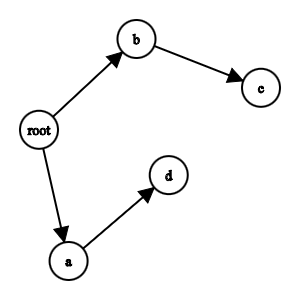
Hope that clarifies the question? Is there a standard name for this type of graph walk and an algorithm to solve it?
- Hamiltonian path
- Finding at most 2 leafs in the graph
CodePudding user response:
I don't know if there's a name for a directed "walkable" graph, but it's not too hard to determine of a graph is walkable or not:
- Find all the strongly connected components using Tarjan's algorithn, for example
- Make a new directed graph of the connections between SCCs. This will be a DAG, and your original graph is walkable if and only if this DAG is walkable.
- To determine whether or not a DAG is walkable, do a topological sort. Then check that each vertex has an edge to the next.
Each of these steps takes linear time, so you get O(|V| |E|) complexity for the whole algorithm.
CodePudding user response:
Theorem: a directed graph is walkable if and only if its strongly connected components are totally ordered by reachability.
Proof sketch: (walkable implies condition) The existence of a walk implies that, for each two strongly connected components, a vertex from one or the other appears first in the walk. That component can reach the other. (condition implies walkable) Since there is full connectivity inside a strongly connected component, each is walkable on its own. We just have to concatenate the walks according to the total order, adding the necessary transitions.
The proof is constructive, so we can extract an algorithm.
Algorithm
- Compute the strongly connected components.
- Concatenate the strongly connected components in topological order. Actually Tarjan's algorithm will list them in reverse topological order, so this doesn't need to be a separate step.
- For each adjacent pair in the previous list, use breadth-first search to find a shortest path.
In general, this algorithm does not find the shortest walk (that's NP-hard by reduction from Hamiltonian path).
