Open the debugger, search xh5_S_KLC_D, debug the diagram below, enter xh5_S_KLC_D method
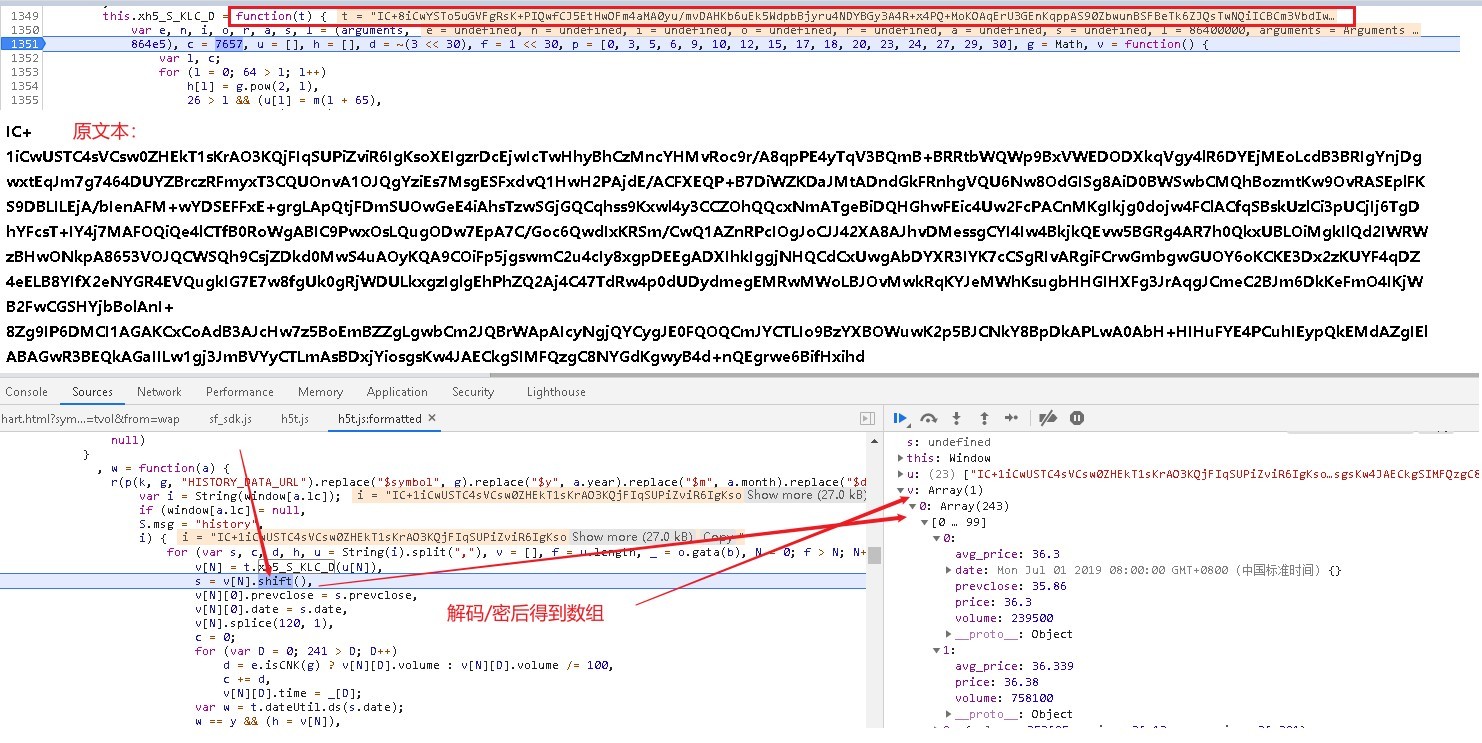
enclosing xh5_S_KLC_D=function (t) {
Var e, n, I, o, r, a, s, l=(the arguments,
864 e5), c=7657, u=[], h=[], d=~ (3 & lt; <30), f=1 & lt; <30, p=[0, 3, 5, 6, 9, 10, 12, 15, 17, 18, 20, 23, 24, 27, 29, 30], g=Math, v=function () {
,
N [l + "_" + a]=(7 & amp; R) + o (" m "+ a),
Break
}
If (a=15 & amp; R,
0==a? N.d=N ([6]) [0] : 1==a? (o.d=a=N ([1 http://finance.sina.com.cn/sinafinancesdk/js/sf_sdk.js
Consult everybody, this is what the decryption algorithm, can be transplanted to other languages? The difficulty?
Reference articles:
Sina's stock system of decryption _ cao _CFA_FinTech_ sina blog
http://blog.sina.com.cn/s/blog_675cd6f60102ygip.html
CodePudding user response:
enclosing xh5_S_KLC_D=function (t) {
Var e, n, I, o, r, a, s, l=(the arguments,
864 e5), c=7657, u=[], h=[], d=~ (3 & lt; <30), f=1 & lt; <30, p=[0, 3, 5, 6, 9, 10, 12, 15, 17, 18, 20, 23, 24, 27, 29, 30], g=Math, v=function () {
Var l, c;
For (l=0; 64 & gt; l; L++)
[l]=g.p h ow (2, l),
26 & gt; L & amp; & (u/l=m (l + 65),
U/l + 26]=m (l + 97),
10 & gt; L & amp; & (u + 52 [l]=m (l + 48)));
For (u.p ush (" + ", "/"),
U=u.j oin (" "),
N=t.s plit (" "),
I=n.l ength,
L=0; i> l; L++)
N [l]=u.i ndexOf (n [l]);
The return o={},
E=a=0,
R={},
C=N ([12, 6]),
S=63 ^ c [1],
{
_1479: M,
_136: A,
_200: k,
_139: O,
_197: _mi_run,
_3466: _k2_run
} [" _ "+ c [0]] | | function () {
Return []
}
}, m=String fromCharCode, b=function (t) {
Return t==={}. _
}, y=function () {
Var t, e;
For (t=_ (),
E=1; ; ) {
if (! _ ())
Return e * (2 * t - 1);
E++
}
}, _=function () {
Var t;
Return e & gt;=I? 0: (t=n [e] & amp; 1 & lt;
A. & gt;=6 & amp; & (a -=6,
E++),
!!!!! T)
}, N=function (t, o, r) {
Var s, l, c, u, d;
For (l=[],
C=0,
O | | (o=[]),
R | | (r=[]),
S=0; S & lt; T.l ength; S++)
If (u=t [s],
C=0,
U) {
If (e & gt;=I)
Return the l;
If (t [s] <=0)
C=0;
Else if (t [s] <30)={
For (; D=6 - a,
D=u & gt; D? D: u,
C |=(n [e] & gt;> A. & amp; (1 & lt;
A. & gt;=6 & amp; & (a -=6,
E++),
U -=d,
! (0 & gt;=u); )
;
O [s] & amp; & C & gt;=h [t] [s] - 1 & amp; & (c - h=[t [s]])
} the else
C=N (t [s] - [30, 30], [s]] of [0, o),
R [s] | | (c=c [0] + [1] c * h [30]);
L [s]=c
} the else
L [s]=0;
Return the l
}, x=function () {
Var t;
Return t=N ([3]) [0],
1==t? (o.d=N ([18], [1]) [0],
T=0) : t | | (t=N ([6]) [0]),
T
{}, w=function (t)
Var e, n, I;
For (t & gt; 1 & amp; & (e=0),
E=0; T & gt; e; E++)
O.d + +,
I=o.d % 7,
(3==I | | 4==I) & amp; & (o.d +=5 - I);
Return n=new Date,
N.s etTime ((c + o.d) * l),
N
{}, S=function (t)
Var e, n, I;
For (I=o.w d | | 62,
E=0; T & gt; e; E++)
Do
O.d + +;
while (! (I & amp; 1 & lt; <7 + 10) (o.d % % 7));
Return n=new Date,
N.s etTime ((c + o.d) * l),
N
{}, T=function (T)
Var e, n, I;
Return the t? 0 & gt; T? (e=T (T),
[[0] - e - e [1]]) : (e=t % 3,
N=(t - e)/3,
I=(n, n),
E & amp; & I [1] e + +,
I) : [0, 0]
}, C=function (t, e, n) {
Var I, o, r;
For (o===typeof e "number"? T (e) : e,
R=T (n),
I=[r [0] - [0], o r [1] - [1]] o,
O=1; I [0] O *=5,
I [1] -;
For (; I [1] O *=2,
I [0] -;
If (o & gt; 1 & amp; & (t *=o),
I=[0], I
T=_decnum (t),
0 & gt; I) {
For (; T.l ength + I & lt;=0; )
T="0" + t;
Return the I +=t.l ength,
O=t.s ubstr (0, I) - 0,
Void 0===n? O + "" + t.s ubstr (I) - 0: (r=tc harAt (I) - 0,
R & gt; 5? O++ : 5==r & amp; & (t.s ubstr (I + 1) - 0 & gt; 0? O++ : o +=1 & amp; O),
O)
}
For (; i> 0; I -)
T +="0";
Return t - 0
}, k=function () {
Var t, n, r, a, l;
If (s & gt;
=1)return [];
For (o.d=N ([18], [1]), [0] - 1
R=N ([3, 3, 30, 6]),
O.p=r [0],
O.l d=r [1],
O. chua d=r [2],
O. chua=r [3],
O.m=g.p ow (10, o.p),
O.p c=o. chua d/o.m,
N=[],
T=0; A={
D: 1
},
_ () & amp; & (r=N ([3]) [0],
0==r? A. d.=N ([6]) [0] : 1==r? (o.d=N ([18]) [0],
A. d.=0) : a. d.=r),
L={
Date: w (a. d.)
},
_ () & amp; & (o.l d +=y ()),
R=N (3 * o.l [d], [1]),
O. chua d +=r [0],
nullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnull 