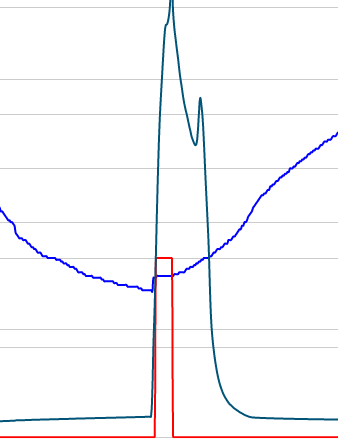
Requirements: this is the data on the front end through echarts now I need to show out the shape of the article according to the previous data to determine the current state of the data points
Try: 1. Baidu before using least square method for fitting curve but feel slope does not return, don't know if there is something wrong in my understanding of the return value of the local
My function:

 
///& lt; Summary> 
///using the least squares fitting binary multiple curve 
///& lt;/summary> 
///& lt; Param name="arrX & gt;" X coordinate of known points set & lt;/param> 
///& lt; Param name="' arrY & gt;" The y coordinate of known points set & lt;/param> 
///& lt; Param name="length" & gt; The number of known points & lt;/param> 
///& lt; Param name="dimension" & gt; Maximum number of equation & lt;/param> 

Private double [] MultiLine (double [] arrX, double [] 'arrY, int length, int dimension)//binary multiple linear equation fitting curve 
{
Int n=dimension + 1;//dimension equation needs dimension coefficient of + 1 
Double [and] Guass=new double [n, n + 1); For example://gaussian matrix y=a0 + a1 + a2 * * x x x x 
for (int i=0; I & lt; n; I++) 
{
Int j; 
For (j=0; J & lt; n; J++) 
{
Guass [I, j]=SumArr (arrX, j + I, length); 
} 
Guass [I, j]=SumArr (arrX, I, 'arrY, 1, length); 
} 

Return ComputGauss (Guass, n); 

} 


Private double SumArr (double [] arr, int n, int length)/n/o array elements and 
{
Double s=0; 
for (int i=0; I & lt; length; I++) 
{
If (arr [I]!=0 | | n!=0) 
S=s + math.h Pow (arr [I], n); 
The else 
S=s + 1; 
} 
Return s; 
} 
Private double SumArr (double [] arr1, int n1, double [] arr2, int n2, int length) 
{
Double s=0; 
for (int i=0; I & lt; length; I++) 
{
If ((arr1 [I]!=0 | | n1!=0) & amp; & (arr2 [I]!=0 | | n2!=0)) 
S=s + math.h Pow (arr1 [I], n1) * math.h Pow (arr2 [I], n2); 
The else 
S=s + 1; 
} 
Return s; 

} 

Private double [] ComputGauss (double [and] Guass, int n) 
{
int i, j; 
Int k, m; 
Double temp. 
Double Max; 
Double s; 
Double x=new double [] [n]. 

For (I=0; I & lt; n; I++) x [I]=0.0;//initialize 


For (j=0; J & lt; n; J++) 
{
Max=0; 

K=j; 
For (I=j; I & lt; n; I++) 
{
If (Math. Abs (Guass [I, j]) & gt; Max) 
{
Max=Guass (I, j), 
K=I; 
} 
} 
If (k!=j) 
{
For (m=j; M & lt; N + 1; M++) 
{
Temp=Guass [j, m]; 
Guass [j, m]=Guass (k, m), 
Guass [k, m]=temp; 

} 
} 

If (0==Max) 
{
//"the linear equations for singular linear equations" 

return x; 
} 


For (I=j + 1; I & lt; n; I++) 
{

S=Guass (I, j), 
For (m=j; M & lt; N + 1; M++) 
{
Guass [I, m]=Guass [I, m] - Guass [j, m] * s/(Guass [j] j); 

} 
} 


}//end for (j=0; J

For (I=n - 1; I & gt;=0; I -) 
{
S=0; 
For (j=I + 1; J & lt; n; J++) 
{
S=s + Guass [I, j] * x [j]; 
} 

[I]=x (Guass [I, n] -s)/Guass [, I]. 

} 

return x; 
}//the return value is the function of the coefficient of 

CodePudding user response:

I think there's another solution: take a piece of data through the curve of peak and trough values to judge whether a single direction and then set up a band, filtering small fluctuations, do not know if this idea ok

CodePudding user response:

For example://gaussian matrix y=a0 + a1 + a2 * * x x x x

The calculated the

CodePudding user response:

refer to the second floor morning to evening reply:

//gaussian matrix, such as: y=a0 + a1 + a2 * * x x x x

The calculated the

Line 12 is composed of two yuan a data source, I understand, then the following data will compute the matrix

CodePudding user response:

I mean you this return 3 coefficient a0, a1, a2 into computing fitting curve not

You the fitting curve and original curve under the contrast, look at it?

CodePudding user response:

Reference

now I need to the shape of the article according to the previous data to determine the current state of the data points

I guess you're moving average

The basic painting in the "timing signal processing", in theory, of course, which has a complete theory "difference equation", "return to trend", I guess you don't want to see

From the description, you might just want to make a simple resampling (moving average), but we don't know what exactly do you want to do, so can only tell you can use the utility class
Usually can use the tools
1. Mathnet -- -- -- -- -- -- -- -- -- -- - signal processing, hamming window, resampling, data fitting, the regression predict
2. AccordNET -- -- -- -- -- -- -- -- -- -- - is also a kit, but he signal processing of this part on the audio sampling (because of audio sampling is timing signal, the library put signal processing abstract audio signal of the signal, complex signal composite signal)

CodePudding user response:

reference 4 floor morning to evening reply:

I mean, you this return 3 coefficient a0, a1, a2 into computing fitting curve not

You the fitting curve and original curve under the contrast, look at it?

Do this is before I directly according to the returned coefficient to judge the to this respect is not very understand the original is I made a mistake and source curve fitting curve comparison will be the trend for me have a try? Thank you

CodePudding user response:

Because we don't know what you want, can only try to give some speculation on the side and can use the tool

https://blog.csdn.net/qq_19600291/article/details/101010249

For example, this article is "moving average filter," if you want to do this thing, mathnet, AccordNET both kits we can complete this function

CodePudding user response:

Each set of data contrast each change of contiguous data, find out the biggest change value, and comparing the several groups of data of the maximum change don't come out? (contrast is stepped up that point)