Adding 2 vectors and comparing the angle of the result to both vectors does not give same result. Wh-CodePudding

I want to calculate the angle between vectors. I thought the sum of 2 vectors should be in the middle of the 2. But calculating the angle with my method gives different results. I guess it has to be with rounding but the result is too different. I tried 2 different approaches. Can you explain me, why? Or am I wrong with my math understanding?

from numpy import (array, dot, arccos, clip, sum)
from numpy.linalg import norm
import spectral
import numpy as np


def calculateAngle(u, v):
    c = dot(u, v) / norm(u) / norm(v)  # -> cosine of the angle
    angle = arccos(clip(c, -1, 1))  # if you really want the angle
    return c, angle


def calc_with_numpy():
    print("Method 2:")

    v = (u1_norm   u2_norm)
    c1, angle1 = calculateAngle(u1, v)
    c2, angle2 = calculateAngle(u2, v)

    print("angle1:", angle1)
    print("angle2:", angle2)

def calc_with_spectral():
    print("Method 1:")
    v = (u1_norm   u2_norm)
    img=np.array([v]).reshape((1,1,v.size))
    means = np.array([u1, u2])
    angles = spectral.spectral_angles(img, means)
    print("angle1:", angles[0,0,0])
    print("angle2:", angles[0, 0, 1])

u1 = array([1.0,2.0], dtype="float64")
u1_norm = u1 / sum(u1)
u2 = array([3.0,2.0], dtype="float64")
u2_norm = u2 / sum(u2)

calc_with_spectral()
calc_with_numpy()

My results:

Method 1:

angle1: 0.25518239062081866

angle2: 0.2639637236257044

Method 2:

angle1: 0.2551823906208191

angle2: 0.2639637236257044

CodePudding user response：

You are wrong here

u1_norm = u1 / sum(u1)
u2_norm = u2 / sum(u2)

To get normalized (unit length) vector, you need to divide it's components by vector length, not by component sum (like you perform right job inside calculateAngle)

u1_norm = u1 / np.linalg.norm(u1)

CodePudding user response：

just extchange the following code

u1_norm = u1 / sum(u1)
u2_norm = u2 / sum(u2)

u1_norm = u1 / len(u1)
u2_norm = u2 / len(u2)

CodePudding user response：

You've normalised wrong. Instead, do

u1_norm = u1 / np.sqrt(np.sum(u1**2))
u2_norm = u2 / np.sqrt(np.sum(u2**2))

I now get

>>> calc_with_numpy()
angle1: 0.2595730571232615
angle2: 0.2595730571232615
>>> norm(u1) == np.sqrt(np.sum(u1**2))
True
>>> norm(u2) == np.sqrt(np.sum(u2**2))
True

I don't know what spectral is, my python distribution doesn't have it as a module.

CodePudding user response：

This function can be used to compute the angle (in degrees) with the x axis of a 2d vector [x, y]:

from math import atan2, pi

def angle(vec):
    return atan2(*reversed(vec)) * 180 / pi

Now if you want to compute the angle between two vectors, you can use this function:

def angle_between_vecs(vec1, vec2):
    return abs(angle(vec1) - angle(vec2))

You may also want to compute the sum of two vectors:

def sum_vecs(vec1, vec2):
    return [vec1[0]   vec2[0], vec1[1]  vec2[1]]

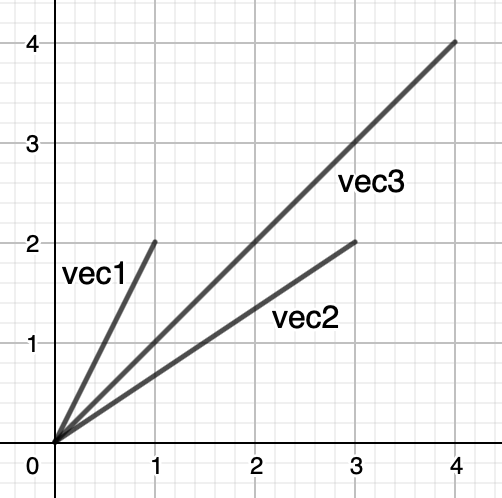
Now notice that angle(sum_vecs(vec1, vec2)) is not necessarily equal to angle_between_vecs(vec1, vec2). Look at this graphical example that follows (vec3 is the sum of vec1 and vec2). As you can see, the sum is not exactly cutting the angle in two parts.

This code can be clearly optimised by using for example NumPy, but this is just an example to show you that your assumption that the angle of the sum should be between the two vectors is wrong!