Closed. This question needs to be more
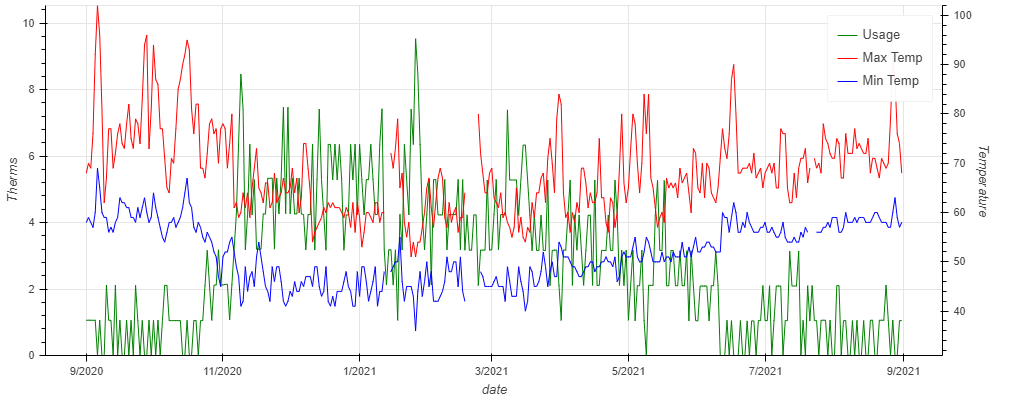
There is appears to be an obvious correlation that as temperatures go down, gas use goes up.
I have both a gas furnace and a gas water heater. What I would like to do is find the baseline usage per day in therms, without the part that fluctuates with temperature. I am assuming that temperature related fluctuation is mostly the furnace and what is left is the water heater. I know that the water heater will fluctuate with outside temp too, but I am assuming it is nominal for this analysis.
I have looked at correlation funcions in numpy and pandas and done stuff like this:
corr_coef = all_data_df['USAGE'].corr(all_data_df['TMIN'])
corr_coef
-0.86344...
then
all_data_df['USAGE'] - corr_coef * all_data_df['TMIN']
DATE
2020-09-01 51.139755
2020-09-02 52.003199
2020-09-03 51.139755
2020-09-04 50.276311
2020-09-05 52.866643
...
2021-08-27 52.866643
2021-08-28 54.396976
2021-08-29 50.943199
2021-08-30 50.266311
2021-08-31 51.129755
But the units seem to be more in the temperature range than in the therms range, which is what I was hoping for. Do I need to scale the units to be similar before subtracting or correlating?
Is there a better way to do this with different analysis? Or am I just wrong that I can isolate the baseline from the temperature related fluctuation?
I prefer an answer that points me to the why instead of just the how if you can :)
Thanks
CodePudding user response:
This is more of a data question than a programming one. You'll have to decide how to calculate the "temperature contribution". The simplest way would be to do regression on the temperature. Since you have max and min, you might want to do multilinear regression on the two types of temperature. Once you've gotten the coefficients from the regression, you can use them to calculate what the linear contribution of temperature is, and subtract it from the usage. If you want be fancier, you can look at models other than the linear one.
Multiplying the independent variable by the coefficient of correlation is not a correct procedure. Doing is is treating r as if it were the linear coefficient, but the coefficient of correlation is very different from the linear coefficient. The former is a measure of how much of the variation of the dependent variable is "explained" by the independent variable, while the latter is a "conversion factor" that gives how much the dependent variable changes for a unit change in the independent variable. Basically, r tells you how closely the data points are clustered around a straight line, while the linear coefficient tells you what the slope of the line of best fit is.
