numpy - Inverse of a matrix/array filled with Fractions

I am trying to use numpy to perform operations on matrices represented as numpy arrays.
I have Fractions as elements in these matrices.

Seems everything works fine until I try to find the inverse.

This gives an error.

Is this a bug in numpy?

I mean, if numpy allows us to e.g. multiply such Fraction-filled matrices, then it should allows us to find the inverse too, right?

import numpy as np
from fractions import Fraction as F

c = np.array([[F(2),F(-1), F(-1)],[F(3),F(4), F(-2)],[F(3),F(-2), F(4)]])

c @ c

np.dot(c, c)

np.linalg.inv(c)

Error:

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-45-5ed58b2836e1> in <module>
----> 1 np.linalg.inv(c)

<__array_function__ internals> in inv(*args, **kwargs)

C:\Programs\Anaconda3\lib\site-packages\numpy\linalg\linalg.py in inv(a)
    544     signature = 'D->D' if isComplexType(t) else 'd->d'
    545     extobj = get_linalg_error_extobj(_raise_linalgerror_singular)
--> 546     ainv = _umath_linalg.inv(a, signature=signature, extobj=extobj)
    547     return wrap(ainv.astype(result_t, copy=False))
    548 

TypeError: No loop matching the specified signature and casting was found for ufunc inv

My numpy version is

1.19.2

CodePudding user response：

I agree with the other answer. Numpy is for numerics meaning imperfect calculations with floats. If you want to do precise aka symbolic calculations. You should use sympy instead. E.g. try:

import sympy
from fractions import Fraction as F

c = sympy.Matrix([[F(2),F(-1), F(-1)],[F(3),F(4), F(-2)],[F(3),F(-2), F(4)]])
c.inv()

CodePudding user response：

Not sure if you can call it a bug, seems to be working as intended. Numpy's linalg module is a light version of Scipy's linalg module; Numpy only supports floats or complex floats (edit: unless you're using what Numpy internally calls an 'exact type', like int; those are casted). Even Scipy doesn't support fractions. From the source code of Scipy's linalg (emphasis mine):

Many SciPy linear algebra functions do support arbitrary array-like input arguments. Examples of commonly unsupported inputs include matrices containing inf/nan, sparse matrix representations, and matrices with complicated elements

Reading the source code, Numpy is more restrictive; Scipy accepts anything where calling np.array(A) does not produce an array with dtype object. Whether this makes sense is subjective; it seems there's some nontrivial compatibility (with existing C algorithms) or performance tradeoffs to allowing general objects in the arrays.

CodePudding user response：

In [291]: import fractions
In [292]: F = fractions.Fraction
In [293]: c = np.array([[F(2),F(-1), F(-1)],[F(3),F(4), F(-2)],[F(3),F(-2), F(4)]])
     ...: 
In [294]: c
Out[294]: 
array([[Fraction(2, 1), Fraction(-1, 1), Fraction(-1, 1)],
       [Fraction(3, 1), Fraction(4, 1), Fraction(-2, 1)],
       [Fraction(3, 1), Fraction(-2, 1), Fraction(4, 1)]], dtype=object)
In [295]: c@c
Out[295]: 
array([[Fraction(-2, 1), Fraction(-4, 1), Fraction(-4, 1)],
       [Fraction(12, 1), Fraction(17, 1), Fraction(-19, 1)],
       [Fraction(12, 1), Fraction(-19, 1), Fraction(17, 1)]], dtype=object)

This works because the elements of c support simple multiplication and addition.

In [298]: c[0,0]*c[1,1]
Out[298]: Fraction(8, 1)

Compare the time for this object dtype matrix multiplication:

In [300]: timeit c@c
123 µs ± 523 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)

With the time for a float dtype multiplication:

In [301]: c1=c.astype(float)
In [302]: c1
Out[302]: 
array([[ 2., -1., -1.],
       [ 3.,  4., -2.],
       [ 3., -2.,  4.]])
In [303]: timeit c1@c1
4.19 µs ± 28.7 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

With a numeric dtype, @/dot passes the task onto fast compiled libraries. For object dtype it has to perform a slower python-level calculation.

inv has the fast numeric mode, but has not implemented the slow object version.

With object dtype input the full error message is:

UFuncTypeError: Cannot cast ufunc 'inv' input from dtype('O') to dtype('float64') with casting rule 'same_kind

With a float dtype:

In [304]: np.linalg.inv(c1)
Out[304]: 
array([[ 0.2       ,  0.1       ,  0.1       ],
       [-0.3       ,  0.18333333,  0.01666667],
       [-0.3       ,  0.01666667,  0.18333333]])
In [305]: timeit np.linalg.inv(c1)
16.4 µs ± 339 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Compare that to the sympy version offered by https://stackoverflow.com/a/69239281/901925

In [308]: import sympy
In [309]: from fractions import Fraction as F
     ...: 
     ...: c = sympy.Matrix([[F(2),F(-1), F(-1)],[F(3),F(4), F(-2)],[F(3),F(-2), F(4)]])
In [310]: c
Out[310]: 
Matrix([
[2, -1, -1],
[3,  4, -2],
[3, -2,  4]])
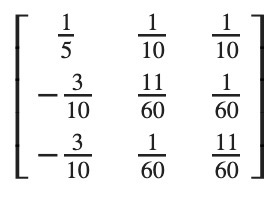
In [311]: c.inv()
Out[311]: 
Matrix([
[  1/5,  1/10,  1/10],
[-3/10, 11/60,  1/60],
[-3/10,  1/60, 11/60]])
In [312]: timeit c.inv()
801 µs ± 23.2 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

scipy is more explicit

In [315]: from scipy import linalg
In [316]: linalg.inv(c)
Traceback (most recent call last):
  File "<ipython-input-316-48147545516b>", line 1, in <module>
    linalg.inv(c)
  File "/usr/local/lib/python3.8/dist-packages/scipy/linalg/basic.py", line 939, in inv
    a1 = _asarray_validated(a, check_finite=check_finite)
  File "/usr/local/lib/python3.8/dist-packages/scipy/_lib/_util.py", line 296, in _asarray_validated
    raise ValueError('object arrays are not supported')
ValueError: object arrays are not supported