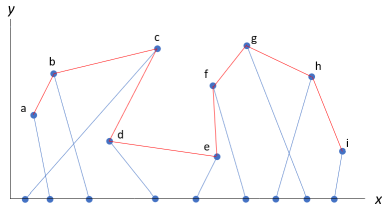
I have a list of perhaps hundreds of unsorted 2D line segments at random angles as shown in blue above, and I need to determine the sorted sequence of points a – i from them as shown in red. Here are some constraints and observations:
- The red polyline sequence a - i forms a tight enclosure of the outer points of all the segments. It's like a convex hull, but "sucked" into concavities. A tight enclosure of the entirety of all segments would be a fine solution; I can delete the unused parts.
- An enclosure does exist. The segments are not completely random.
- The y value of one point of each segment is 0, and the other end is a point on the enclosure.
- The enclosure cannot cross any line segment or itself. This also means that all segments are on one side of the enclosure polyline.
- There will be either one or two enclosure segments connected to each enclosure point a - i.
- The points may be spaced widely differently, not as tidily as shown.
- I should be able to determine point a or i if necessary to start off the algorithm.
It seems like starting from a bounding box around all segments and shrinking it to form a tight enclosure would be a reasonable approach, but I can't come up with a decent algorithm. This will eventually be coded in C#, but an algorithm or pseudo-code would be fine.
CodePudding user response:
History: this answer is now marked community wiki. The original conjecture was proven wrong by 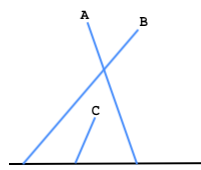
A and B cross, so reversing the x comparison, A is before B. C doesn't cross A or B, so comparing the x values at the bottom, B is before C and C is before A. This creates a rock-paper-scissors situation: A before B, B before C, and C before A. Such intransitive comparisons will cause a comparison sort to fail miserably.