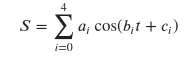Using numpy broadcasting to compute the partial sum of a series-CodePudding

I have to compute the following sum, S defined as:

I have tried the following as a function:

import numpy as np
a = np.array([0.4,2.6,3, 1.2, 3.4])
b = np.array([-5,7,2,1.1,1.8])
c = np.array([3.3,30,15,0.4,28])
t = np.linspace(0, np.pi, 600)
def S(t):
  return np.sum([a[i]*np.cos(b[i]*t   c[i]) for i in range(5)], axis=0)

This works just fine. But I wonder if there is pure numpy version that uses broadcasting without relying on Python's list comprehension?

I have tried:

def S(t):
  return np.sum(a*np.cos(b*t   c), axis=0)

When I compue S(t) I get the following error:

...
ValueError: operands could not be broadcast together with shapes (5,) (600,)

How can I get this to work properly?

CodePudding user response：

How to do it?

For broadcasting you need ones in dimensions you want to have "copied" values. So it works like this:

import numpy as np

a = np.array([0.4,2.6,3, 1.2, 3.4])
b = np.array([-5,7,2,1.1,1.8])
c = np.array([3.3,30,15,0.4,28])
t = np.linspace(0, np.pi, 600).reshape(-1,1)

np.sum(a*np.cos(b*t c), axis=1)

How to check if you did the right thing?

One neat hack you can do is to put sympy.symbols into your arrays and do the same thing. Then you obtain formulas for what it calculated for you:

import sympy

a = np.array(sympy.symbols([f"a{i}" for i in range(5)]))
b = np.array(sympy.symbols([f"b{i}" for i in range(5)]))
c = np.array(sympy.symbols([f"c{i}" for i in range(5)]))
t = np.array(sympy.symbols([f"t{i}" for i in range(10)])).reshape(-1,1)

cos = np.vectorize(sympy.cos)
np.sum(a*cos(b*t c), axis=1)

this gives you

array([a0*cos(b0*t0   c0)   a1*cos(b1*t0   c1)   a2*cos(b2*t0   c2)   a3*cos(b3*t0   c3)   a4*cos(b4*t0   c4),
       a0*cos(b0*t1   c0)   a1*cos(b1*t1   c1)   a2*cos(b2*t1   c2)   a3*cos(b3*t1   c3)   a4*cos(b4*t1   c4),
       a0*cos(b0*t2   c0)   a1*cos(b1*t2   c1)   a2*cos(b2*t2   c2)   a3*cos(b3*t2   c3)   a4*cos(b4*t2   c4),
       a0*cos(b0*t3   c0)   a1*cos(b1*t3   c1)   a2*cos(b2*t3   c2)   a3*cos(b3*t3   c3)   a4*cos(b4*t3   c4),
       a0*cos(b0*t4   c0)   a1*cos(b1*t4   c1)   a2*cos(b2*t4   c2)   a3*cos(b3*t4   c3)   a4*cos(b4*t4   c4),
       a0*cos(b0*t5   c0)   a1*cos(b1*t5   c1)   a2*cos(b2*t5   c2)   a3*cos(b3*t5   c3)   a4*cos(b4*t5   c4),
       a0*cos(b0*t6   c0)   a1*cos(b1*t6   c1)   a2*cos(b2*t6   c2)   a3*cos(b3*t6   c3)   a4*cos(b4*t6   c4),
       a0*cos(b0*t7   c0)   a1*cos(b1*t7   c1)   a2*cos(b2*t7   c2)   a3*cos(b3*t7   c3)   a4*cos(b4*t7   c4),
       a0*cos(b0*t8   c0)   a1*cos(b1*t8   c1)   a2*cos(b2*t8   c2)   a3*cos(b3*t8   c3)   a4*cos(b4*t8   c4),
       a0*cos(b0*t9   c0)   a1*cos(b1*t9   c1)   a2*cos(b2*t9   c2)   a3*cos(b3*t9   c3)   a4*cos(b4*t9   c4)],
      dtype=object)

Notice that this couldn't work with numpy's cosine since that only works for floats. But

cos = np.vectorize(sympy.cos)

gives you a version of sympys cosine that works on arrays elementwise.

CodePudding user response：

I think I found the answer by adding a newaxis to a, b, and c arrays as follows:

def S(t):
   return np.sum(a[:,None]*cos(b[:,None]*t   c[:,None]), axis=0)

def S(t):
   return np.sum(a[:,np.newaxis]*cos(b[:,np.newaxis]*t   c[:,np.newaxis]), axis=0)

Edit:

As suggested by Michael in the comment, a better solution, would be to add a newaxis to t instead (note that in this case the sum is carried out over axis=1):

def S(t):
   return np.sum(a*cos(b*t[:,None]   c), axis=1)