I tried to solve on my own the LeetCode problem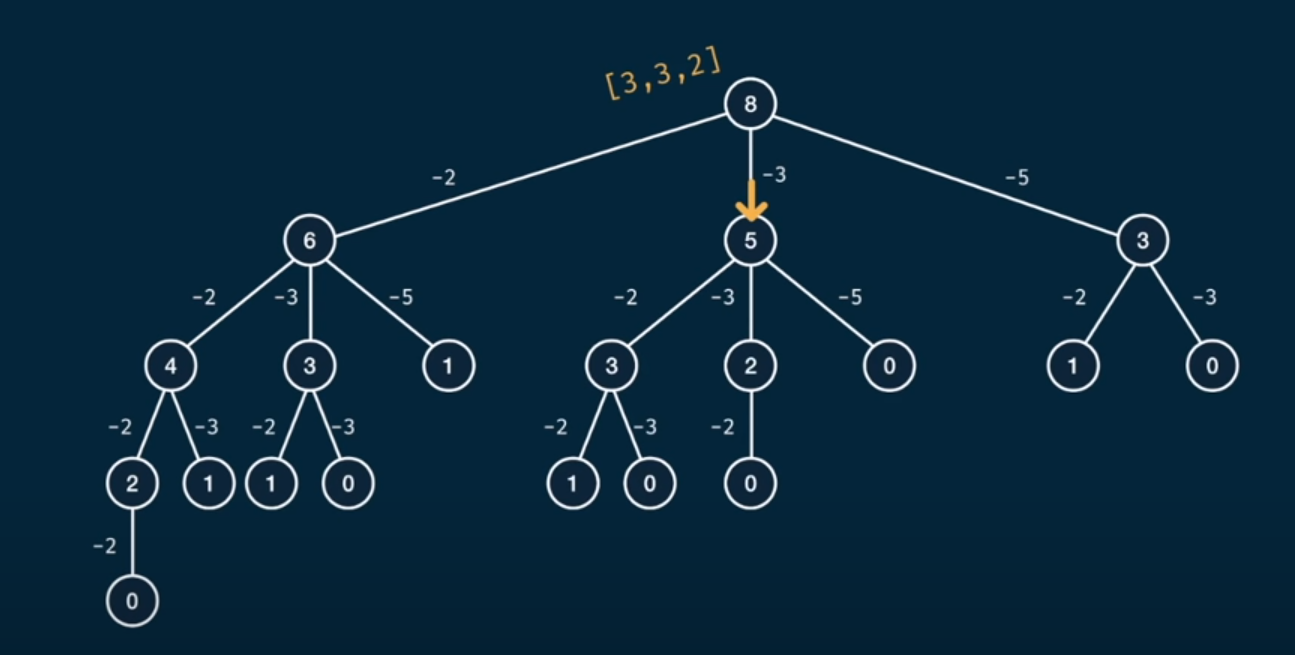

This is my solution:

from typing import List
class Solution:
    def coinChange(self, nums: List[int], target: int) -> int:      
        def dfs(remainder):
            if remainder<0:
                return None
            if remainder==0:
                return []         
            shortest_combination=None
            for num in nums:
                print("target",remainder)
                print("num",num)             
                result=dfs(remainder-num)
                if result!=None:                    
                    combination=[*result,num]                    
                    if shortest_combination==None or len(combination)<len(shortest_combination):                        
                        shortest_combination=combination                    
            return shortest_combination       
        return -1 if dfs(target)==None else len(dfs(target))
    
        
    
s=Solution()
s.coinChange([1,2,5],100)

I print num and remainder, and I see that for some reason remainder never hits 0. Based on DFS, if I keep subtracting 1 from 100 I should be reaching 0, but somehow it does not reach it with any num.

CodePudding user response：

This problem needs to be solved using dynamic programming. Given any value, assume you've already calculated the smallest number of coins to generate 0, ... value - 1, To calculate the smallest number of coins for value, look at the number of coins needed for value - coin1, value - coin2, value - coin3, ..., pick the smallest, and add one.

Actually coding this is something you should do on your own.

CodePudding user response：

Your algorithm is correct, it really does hit 0, but in that case you don't print it (function exits before printing). Adding more debugging you'll see it does reach that base case and backtracks and correctly identifies the sub-solutions.

The problem really is that the tree you are visiting with DFS is exponentially large, whereby you solve the same problem a multitude of times. If you add a few lines of code to implement memoization, you'll see it does the job:

from typing import List

class Solution:
    def coinChange(self, nums: List[int], target: int) -> int:
        memo = {}  # used for memoization
        def dfs(remainder):
            if remainder in memo:  # already solved this problem?
                return memo[remainder]  # then return what we got last time
            if remainder<0:
                return None
            if remainder==0:
                return []         
            shortest_combination=None
            for num in nums:
                result = dfs(remainder-num)
                if result!=None:
                    combination=[*result,num]
                    if shortest_combination==None or len(combination)<len(shortest_combination):
                        shortest_combination=combination                    
            memo[remainder] = shortest_combination  # memoize this solution
            return shortest_combination

        return -1 if dfs(target)==None else len(dfs(target))


s=Solution()
print(s.coinChange([1,2,5],100))  # 20