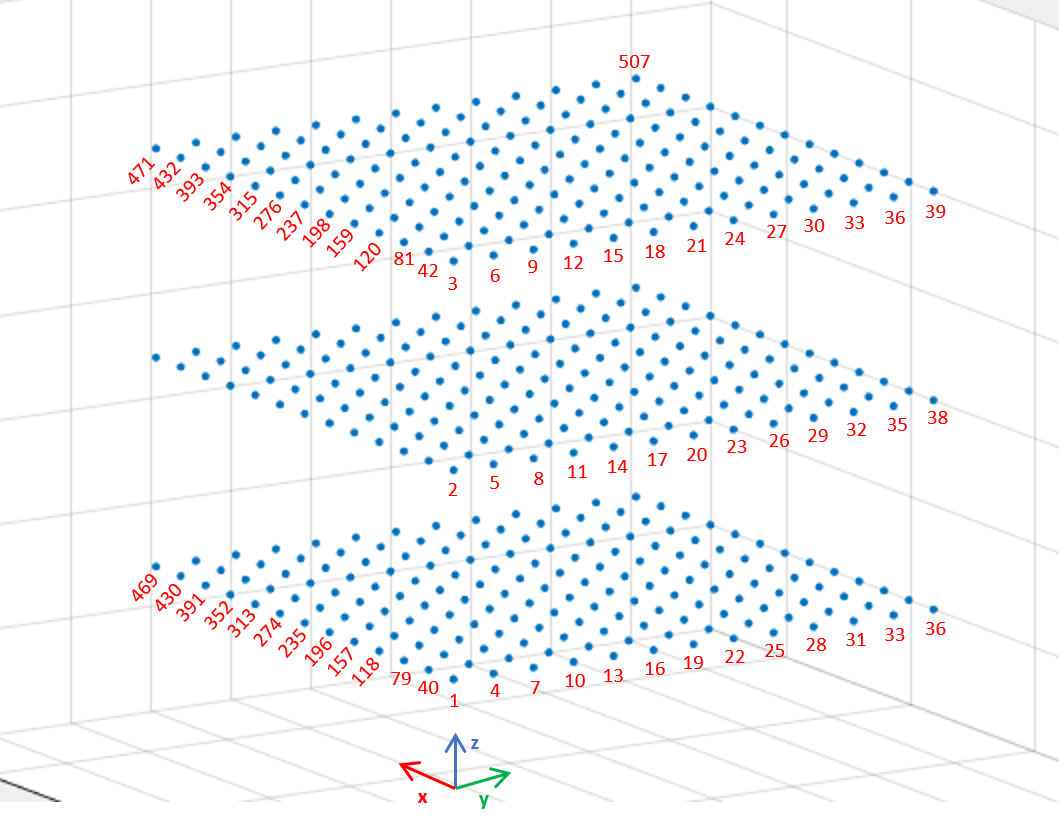
Let’s say I have the following 3D discretized space, in which the indexes of the samples/nodes are sequential as it is shown in the picture.
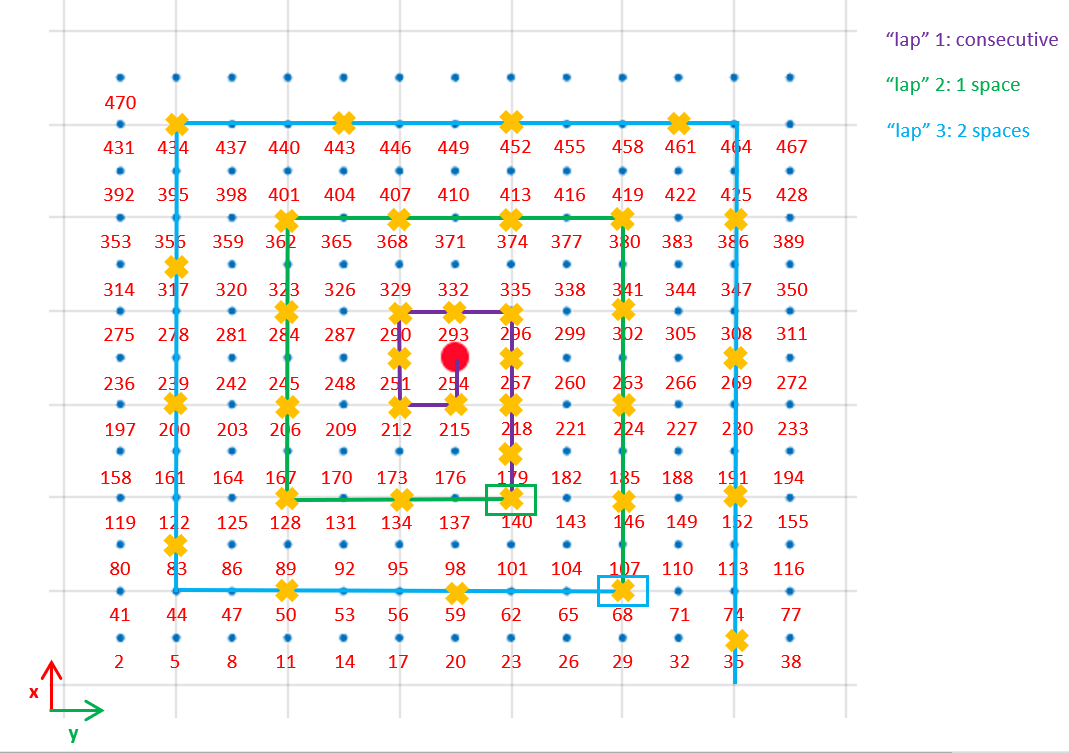
Now consider only the horizontal middle layer.
My objective is to find a programmatically and iterative rule/s that allow me to run a spiral (like the image or similar, it can start in any direction) over the mid-layer, starting from node 254, as it is shown on the image:
As you can see in the picture, the yellow crosses show the nodes to be explored. In the first lap these nodes are consecutive while in the second they are separated by 1 node and so on.
I started to solve the problem as follows (pseudocode):
I considered size(y) = y = 13
Size(z) = z = 3
Lap 1:
- 254 – z * y = 215
- 254 – z * (y 1) = 212
- 254 – z = 251
- 254 z * (y - 1) = 290
- 254 z * y = 293
- 254 z * (y 1) = 296
- 254 z = 257
- 254 – z * (y – 1) = 218
- Lap 2:
- 254 – 3 * z * y = 137
- 254 – 3 * z * (y 2/3) = 131
- …
But I think there may be a simpler, more general rule.
CodePudding user response:
each direction has constant index increment:
const int dx = 39;
const int dy = 3;
const int dz = 1;
so to make a spiral you just start from start index and increment in current direction i-times then rotate by 90 deg and do the same ... then increment i and do this until desired size is hit ...
You should also add range checking so your spiral will not go outside your array as that would screw things up. By checking actual x,y,z coordinates. So either compute them in parallel or infer them from ix using modular arithmetics so for example something like (C ):
const int dx = 39;
const int dy = 3;
const int dz = 1;
int cw[4]={-dx,-dy, dx, dy}; // CW rotation
int ix=254; // start point (center of spiral)
int dir=0; // direction cw[dir]
int n=5; // size
int i,j,k,x,y,z,a; // temp
for (k=0,i=1;i<=n;i =k,k^=1,dir ,dir&=3)
for (j=1;j<=i;j )
{
int a=ix-1;
z = a% 3; a/= 3; // 3 is z-resolution
y = a%13; a/=13; // 13 is y-resolution
x = a;
if ((x>=0)&&(x<13)&&(y>=0)&&(y<13)&&(z>=0)&&(z<3))
{
// here use point ix
// Form1->mm_log->Lines->Add(AnsiString().sprintf("%i (%i,%i,%i) %i",ix,x,y,z,i));
}
ix =cw[dir];
}
producing this output
ix x,y,z i
254 (6,6,1) 1
215 (5,6,1) 1
212 (5,5,1) 2
251 (6,5,1) 2
290 (7,5,1) 2
293 (7,6,1) 2
296 (7,7,1) 3
257 (6,7,1) 3
218 (5,7,1) 3
179 (4,7,1) 3
176 (4,6,1) 3
173 (4,5,1) 3
170 (4,4,1) 4
209 (5,4,1) 4
248 (6,4,1) 4
287 (7,4,1) 4
326 (8,4,1) 4
329 (8,5,1) 4
332 (8,6,1) 4
335 (8,7,1) 4
338 (8,8,1) 5
299 (7,8,1) 5
260 (6,8,1) 5
221 (5,8,1) 5
182 (4,8,1) 5
143 (3,8,1) 5
140 (3,7,1) 5
137 (3,6,1) 5
134 (3,5,1) 5
131 (3,4,1) 5
In case you want CCW spiral either reverse the cw[] or instead of dir do dir--
In case you want to have changeable screw width then you just increment i by the actual width instead of just by one.
CodePudding user response:
Based on @Spektre answer, this code worked for me:
const int x_res = 13;
const int y_res = 13;
const int z_res = 3;
const int dx = 39;
const int dy = 3;
const int dz = 1;
int cw[4]={-dx,-dy, dx, dy}; // CW rotation
int ix=254; // start point (center of spiral)
int dir=0; // direction cw[dir]
int n=30; // size
int i,j,k;
cout << ix << endl;
// first "lap" (consecutive nodes)
for (k=0,i=1;i<=2;i =k,k^=1,dir ,dir&=3)
for (j=1;j<=i;j )
{
ix =cw[dir];
cout << ix << endl;
}
i-=1;
int width = 2; //screw width
i =width;
int dist = 1; //nodes separation
int node_count = 0; //nodes counter
for (k=k,i=i;i<=n;i =k,k^=width,dir ,dir&=3)
{
if (dir==1)
{
dist =1;
}
for (j=1;j<=i;j )
{
ix =cw[dir];
node_count =1;
if ((0 < ix) && (ix <= x_res*y_res*z_res))
{
if (node_count == dist)
{
cout << ix << endl;
node_count = 0;
}
}
else return 0;
}
}
return 0;
with this output:
254 215 212 251 290 293 296 257 218 179 140 134 128 206 284 362 368 374 380 302
224 146 68 59 50 83 200 317 434 443 452 461 386 269 152 35