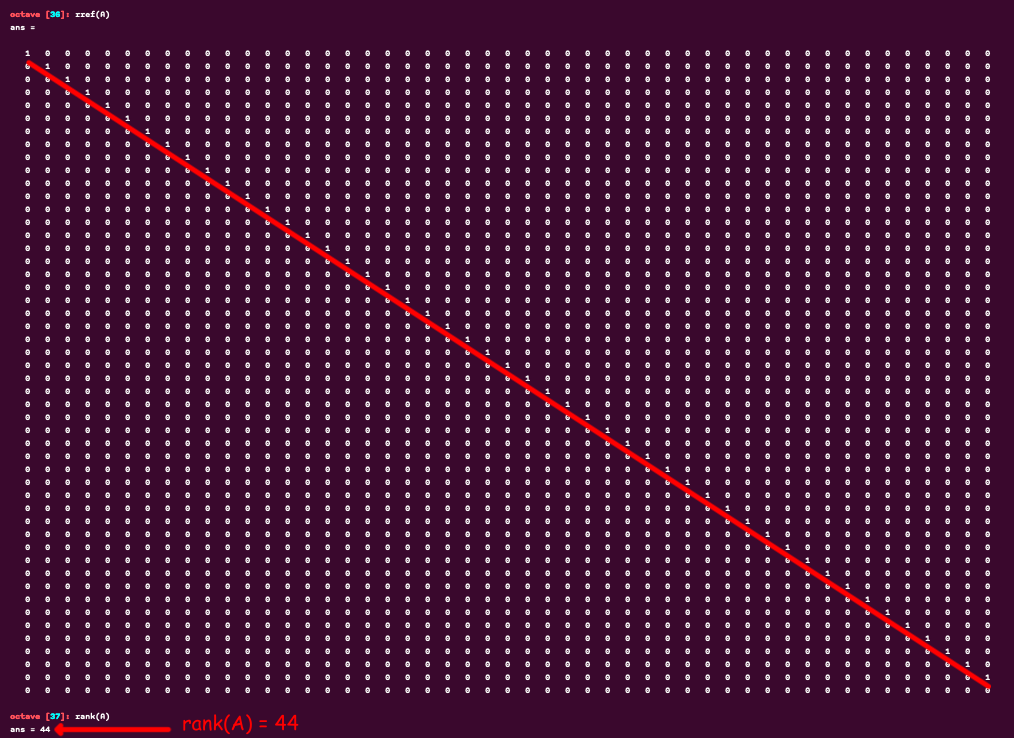
I have 50x49 matrix A that has 49 linearly independent columns. However, my software (octave) tells me its rank is 44:

1. Is it due to some computational error? If so, then how to prevent such errors?

2. If the software was able to correctly calculate rref(A), then why did it fail with rank(A)? Does it mean that calculating rank(A) is more error prone than calculating rref(A), or vice versa? I mean rref(A) actually tells you the rank, but here's a contradiction.

P.S. I've checked, Python makes the same error.

EDIT 1: Here is the matrix A itself. The first 9 columns were given. The rest was obtained with polynomial features.

EDIT 2: I was able to found a similar issue. Here is 10x10 matrix B of rank 10 (and octave calculates its rank correctly). However, octave says that rank(B * B) = 9 which is impossible.

CodePudding user response：

The distinction between an invertible matrix (i.e. full rank) and a non-invertible one is clear-cut in theory, but not so in practice. A matrix B with large condition number (as in your example) can be inverted, but computing the inverse is numerically unstable. It roughly corresponds to B having a determinant that is "small" (using an appropriate, relative measure of "small"), so the matrix is almost singular. As a result, the inverse matrix will be computed with bad accuracy. In your example B, the condition number (computed with cond) is 2.069e9.

Another way to look at this is: when the condition number is large, it well could be that B is "really" singular, but small numerical errors from previous computations make it look barely non-singular. So you can't be sure.

The rank and rref functions use different algorithms (singular-value decomposition for rank, Gauss-Jordan elimination with partial pivoting for rref). For well-behaved matrices the numerical errors will be small in both cases, and the results will be consistent. But for a bad-conditioned matrix the numerical errors will be large and potentially different in each case, giving inconsistent results.

This is a well known issue with numerical algebra. In general, avoid inverting matrices with large condition number.