Problems with sinusoidal curve fitting: amplitude and frequency come out too low-CodePudding

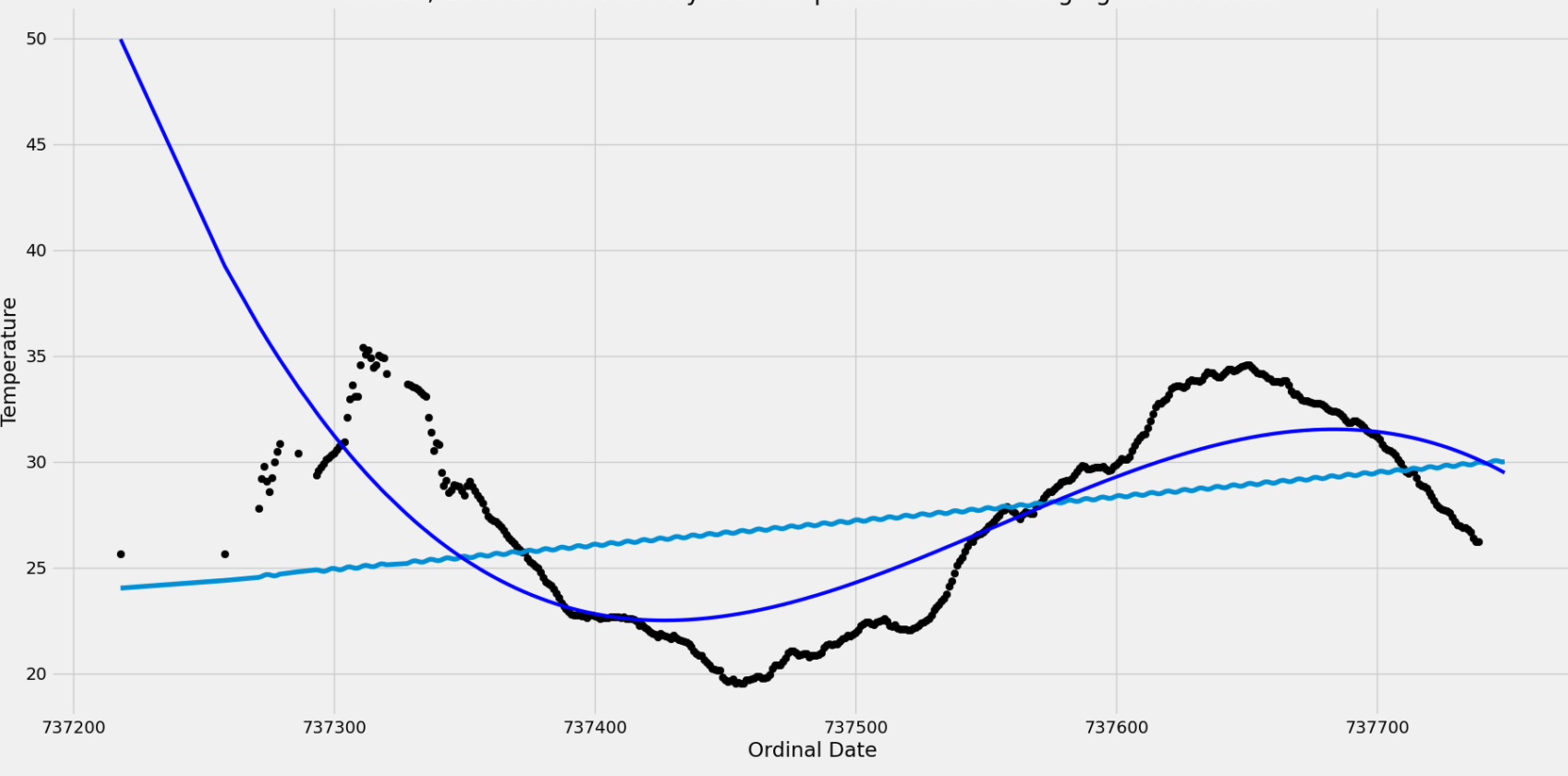
I have some time series data, which corresponds to the black line in the image (it's a rolling mean). I am trying to fit a sinusoidal curve to it with no success; the light blue, almost straight line is the current result. (The dark blue one is a polynomial fit, disregard it for now).

What I tried is this. I got the idea for the function from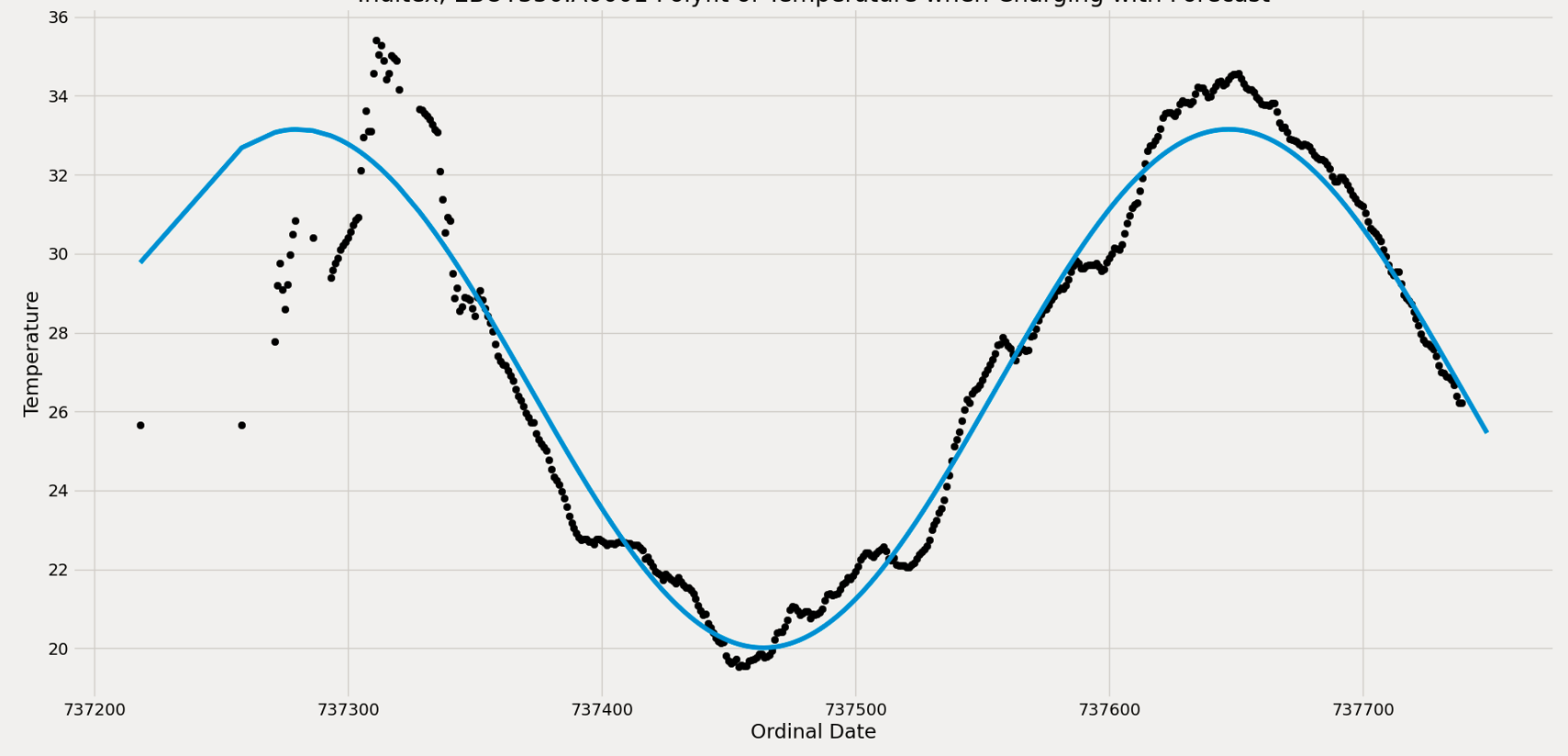

Thank you!

CodePudding user response：

Without data to test, it's hard to tell exactly. However, a good guess is that your starting parameters are off, and then a generalised least squares fit can (easily) fail. You're not even giving curve_fit an initial set of parameters, so the initial starting of a, b, c and d will all be set to 1.

Dealing with only the sinusoidal fit, for your amplitude a, you'll probably want something around 7, and for the offset d, about 27. b is harder to guess, so can be left at 0 (or 1) initially.

But, the quadratic part of the equation will make a mess of things: the x-values are large, so it will change very fast, or rather, c should be very close to zero (close, as in very small, of order 1/x^2, so say ~ 1e-12, to cancel out the effects of the large quadratic variations. Any such small number will have problems fitting as well: normalising your formula / parameters (to be of order 1) beforehand is always a good idea.

In fact, I don't understand why you have a quadratic in your function. Perhaps it's the underlying model that requires this, but the figure itself shows no indication at all of quadratic behaviour. I would remove it.

Finally, while you have an x-offset b, you don't have a parameter for your the period. As a result, it will be fixed at 2π, which it is definitely not. This will be the biggest hurdle in fitting your data, next to the quadratic part of the equation. The period looks to be around 300 (or one year?), or roughly 50 * 2π.

So, try with the following function:

def objective(x, a, b, c, d):
    return a * np.sin(b - c*x/50)   d

with starting parameters of, very roughly:

p0 = [7, 0, 1, 27]

and see what you get.

(If you are wondering about the 50 in the formula: it's not really necessary at these orders of magnitude, but it servers as an example of normalising c to be of order 1. You could so the same for d by replacing it with 10*d and then set its initial guess at 3. Or, if you do that, you can now leave out p0 entirely, with all parameter guesses at 1.)