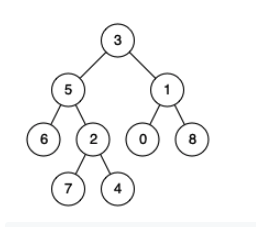
I am trying to solve a problem which is: Find all ancestors of a particular node in a binary tree.
Input: root, targetNode
Output: An array/list containing the ancestors
Suppose, we have the above binary tree as an example. We want to find the ancestors of the node 4. The output should be [3, 5, 2, 4]. If the node is 8, the output is [3, 1, 8]
To solve this, I have written a function which implements DFS.
var ancestor = function(root, target) {
var isFound = false;
const dfs = (node, curr) => {
if (node === null) {
return curr;
}
if (node.val === target.val) {
curr.push(node.val);
isFound = true;
return curr;
}
curr.push(node.val);
const left = dfs(node.left, curr);
if (!isFound) {
const right = dfs(node.right, curr);
curr.pop();
return right;
} else {
curr.pop();
return left;
}
}
console.log(dfs(root, []));
};
But it is not returning the correct ouput. For example, if the targetNode is 7, the output is [3], if the targetNode is 8, the output is also [3]. If I remove the line curr.pop() the output is also invalid. for targetNode 7 it is [3 , 5, 6, 2, 7]. I think I found the issue where I am making mistake. While backtracking, I am doing something wrong with the remove of the node that was pushed in the curr array. If I pass a string instead of the array, it prints the output correctly.
var ancestor = function(root, target) {
var isFound = false;
const dfs = (node, curr) => {
if (node === null) {
return curr;
}
if (node.val === target.val) {
curr = node.val;
isFound = true;
return curr;
}
const left = dfs(node.left, curr node.val '->);
if (!isFound) {
const right = dfs(node.right, curr node.val '->);
return right;
} else {
return left;
}
}
console.log(dfs(root, ''));
The above code with string instead of array prints the output correctly, If I pass targetNode 7, output is 3->5->2->7
My question is, how to properly unchoose/backtrack here? Or is there anything else that I am doing incorrectly? Thanks in advance.
CodePudding user response:
recursion in its natural setting
Recursion is a functional heritage and so using it with functional style yields the best results. This means avoiding imperative things such as mutations like push and cur = node.val, variable reassignments like isFound = true, and other side effects. We can write ancestor as a simple generator-based function that prepends each node to the output of recursive sub-problem -
const empty =
Symbol("tree.empty")
function node(val, left = empty, right = empty) {
return { val, left, right }
}
function* ancestor(t, q) {
if (t == empty) return
if (t.val == q) yield [t.val]
for (const l of ancestor(t.left, q)) yield [t.val, ...l]
for (const r of ancestor(t.right, q)) yield [t.val, ...r]
}
const mytree =
node(3, node(5, node(6), node(2, node(7), node(4))), node(1, node(0), node(8)))
for (const path of ancestor(mytree, 7))
console.log(path.join("->"))3->5->2->7
use modules
To finish, I would recommend a module-based approach for this code -
// tree.js
const empty =
Symbol("tree.empty")
function node(val, left = empty, right = empty) {
return { val, left, right }
}
function* ancestor(t, q) {
if (t == empty) return
if (t.val == q) yield [t.val]
for (const l of ancestor(t.left, q)) yield [t.val, ...l]
for (const r of ancestor(t.right, q)) yield [t.val, ...r]
}
function insert(t, val) {
// ...
}
function remove(t, val) {
// ...
}
function fromArray(a) {
// ...
}
// other tree functions...
export { empty, node, ancestor, insert, remove, fromArray }
// main.js
import { node, ancestor } from "./tree.js"
const mytree =
node(3, node(5, node(6), node(2, node(7), node(4))), node(1, node(0), node(8)))
for (const path of ancestor(mytree, 7))
console.log(path.join("->"))
3->5->2->7
private generator
In the previous implementation, our module exposes a generator for ancestor's public interface. Another option is to return undefined when a node cannot be found and has no ancestry. Consider this alternate implementation which hides the generator and requires the caller to null-check the result instead -
const empty =
Symbol("tree.empty")
function node(val, left = empty, right = empty) {
return { val, left, right }
}
function ancestor(t, q) {
function* dfs(t) {
if (t == empty) return
if (t.val == q) yield [t.val]
for (const l of dfs(t.left)) yield [t.val, ...l]
for (const r of dfs(t.right)) yield [t.val, ...r]
}
return Array.from(dfs(t))[0]
}
const mytree =
node(3, node(5, node(6), node(2, node(7), node(4))), node(1, node(0), node(8)))
const result =
ancestor(mytree, 7)
if (result)
console.log(result.join("->"))
else
console.log("no result")3->5->2->7
CodePudding user response:
You need to check whether the DFS of the right child has found the node. fix:
const left = dfs(node.left, curr);
if (!isFound) {
const right = dfs(node.right, curr);
if(isFound) {
return right;
}
curr.pop();
return; // return nothing, backtracking
}
return left;
CodePudding user response:
In the array example, your loop iterates through the nodes in a DFS manner, so each of those nodes are connected in that manner. If we count the tree nodes in DFS algorithm, [3 , 5, 6, 2, 7] are actually in order 1, 2, 3, 4 and 5. In this manner, your whole tree in an array should be looking like this; [3 , 5, 6, 2, 7, 4, 1, 0, 8].
So when you find the target value, you pop from the current node and trace it all back up to the head node in DFS algorithm.
I'd either suggest finding a way to get around that, or you could save each of these node's parents. Meaning you could use tuples instead of int arrays (if that's acceptable). An index could look like this = (node value, parent value)
[(3,NULL),(5,3),(6,5),(2,5)...]
And then traceback accordingly...