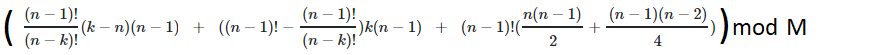I would like to write this formula in C language:

(2<=n<=1e5), (1<=k<=n), (2<=M<=1e9).

I would like to do this without using special structures. Unfortunately in this formula there are a lot of cases which effectively make modulation difficult. Example: ((n-k)!) mod M can be equal to 0, or ((n-1)(n-2))/4 may not be an integer. I will be very grateful for any help.

CodePudding user response：

The expression implies the use of a floating point type. Therefore, use the function fmod to get the remainder of the division.

CodePudding user response：

(n−1)!/(n−k)! can be handled by computing the product (n−k 1)…(n−1).

(n−1)! (n−1)(n−2)/4 can be handled by handling n ≤ 2 (0) and n ≥ 3 (3…(n−1) (n−1)(n−2)/2) separately.

Untested C :

#include <cassert>
#include <cstdint>

class Residue {
public:
  // Accept int64_t for convenience.
  explicit Residue(int64_t rep, int32_t modulus) : modulus_(modulus) {
    assert(modulus > 0);
    rep_ = rep % modulus;
    if (rep_ < 0)
      rep_  = modulus;
  }

  // Return int64_t for convenience.
  int64_t rep() const { return rep_; }
  int32_t modulus() const { return modulus_; }

private:
  int32_t rep_;
  int32_t modulus_;
};

Residue operator (Residue a, Residue b) {
  assert(a.modulus() == b.modulus());
  return Residue(a.rep()   b.rep(), a.modulus());
}

Residue operator-(Residue a, Residue b) {
  assert(a.modulus() == b.modulus());
  return Residue(a.rep() - b.rep(), a.modulus());
}

Residue operator*(Residue a, Residue b) {
  assert(a.modulus() == b.modulus());
  return Residue(a.rep() * b.rep(), a.modulus());
}

Residue QuotientOfFactorialsMod(int32_t a, int32_t b, int32_t modulus) {
  assert(modulus > 0);
  assert(b >= 0);
  assert(a >= b);
  Residue result(1, modulus);
  // Don't initialize with b   1 because it could overflow.
  for (int32_t i = b; i < a; i  ) {
    result = result * Residue(i   1, modulus);
  }
  return result;
}

Residue FactorialMod(int32_t a, int32_t modulus) {
  assert(modulus > 0);
  assert(a >= 0);
  return QuotientOfFactorialsMod(a, 0, modulus);
}

Residue Triangular(int32_t a, int32_t modulus) {
  assert(modulus > 0);
  return Residue((static_cast<int64_t>(a)   1) * a / 2, modulus);
}

Residue F(int32_t n, int32_t k, int32_t m) {
  assert(n >= 2);
  assert(n <= 100000);
  assert(k >= 1);
  assert(k <= n);
  assert(m >= 2);
  assert(m <= 1000000000);
  Residue n_res(n, m);
  Residue n_minus_1(n - 1, m);
  Residue n_minus_2(n - 2, m);
  Residue k_res(k, m);
  Residue q = QuotientOfFactorialsMod(n - 1, n - k, m);
  return q * (k_res - n_res) * n_minus_1  
         (FactorialMod(n - 1, m) - q) * k_res * n_minus_1  
         (n > 2 ? QuotientOfFactorialsMod(n - 1, 2, m) *
                      (n_res * n_minus_1   Triangular(n - 2, m))
                : Residue(1, m));
}