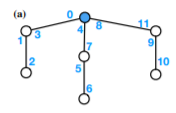
So I have a G directed graph (directed in both ways from a node v), and its Euler tour labelling, like this:

I have a function, called root(written_L,u), where u is the new root of the target graph/component, and written_L is an Euler tour labelling. So the root function makes the u node the root, and recalculates all the edge labels, giving a new Euler tour labelling.

However, I can't totally understand the algorithm given for the root function:

And the corresponding denotement system:

I tried to make a program for this problem, but I couldn't totally understand these mathematical expressions. I would appreciate it if someone could explain to me all these meanings in a non-mathematical form. Furthermore, feel free to ask for more information if needed.

CodePudding user response：

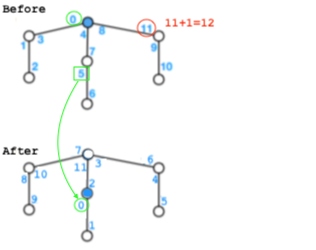
Sometimes all you need is an example. The image below shows the edge labelling after moving the root node to the middle of the center column.

You'll notice that all we did is subtract 5 from all the numbers. That's great when the original label is at least 5. When the original label is less than 5, we need to subtract 5 and then add 12, to keep the label in the range 0 to 11.

So for example, the edge that used to be labelled 8 is relabelled as 8-5=3. And the edge that was labelled 4 is relabelled as 4 -5 12 = 11.

The other thing you need to know is that subtracting 5 (keeping the result in the range 0 to 11) is the same as adding 7 modulo 12. Repeating the same examples, 8 is relabelled (8 7) % 12 = 3, and 4 is relabelled (4 7) % 12 = 11.

So the algorithm is:

• Find the largest label entering the original root, and add 1 to find the modulo (M). In the example the largest label is 11, so M is 12.
• Find the smallest label leaving the new root (Z). In the example Z is 5.
• Compute the delta (D) as D = M - Z. In the example, D is 7.
• Update every label (L) using the formula newL = (L D) % M