How does a recursive function inside a while loop works in Java?-CodePudding

I found this code on google but i couldn't find how does the recursive part actually work. The code is about finding the possible path between 2 vertices on a directed graph. Here is the method to print the total possible path :

public void  total_path(int source, int destination)
{
  result = 0;
  boolean[] visit = new boolean[size];
  for(int i = 0; i < size; i  )
  {
    visit[i] = false;
  }
  count_path(source, destination, visit);
  System.out.println(result);
}

Here is the recursive method to count all possible paths :

  public void  count_path(int start, int end, boolean[] visit)
     {
              if(start > size || end > size || start < 0 || end < 0 || node == null)
              {
                return ;
              }
        
              if(visit[start]==true)
              {
                return;
              }
        
              if(start == end)
              {
                 result = result   1;
              }
              
              visit[start] = true;
              AjlistNode temp = node[start].next;
        
              while(temp!=null)
              {
                count_path(temp.id, end, visit); 
                temp = temp.next;
              }
              
              visit[start]=false;
     }

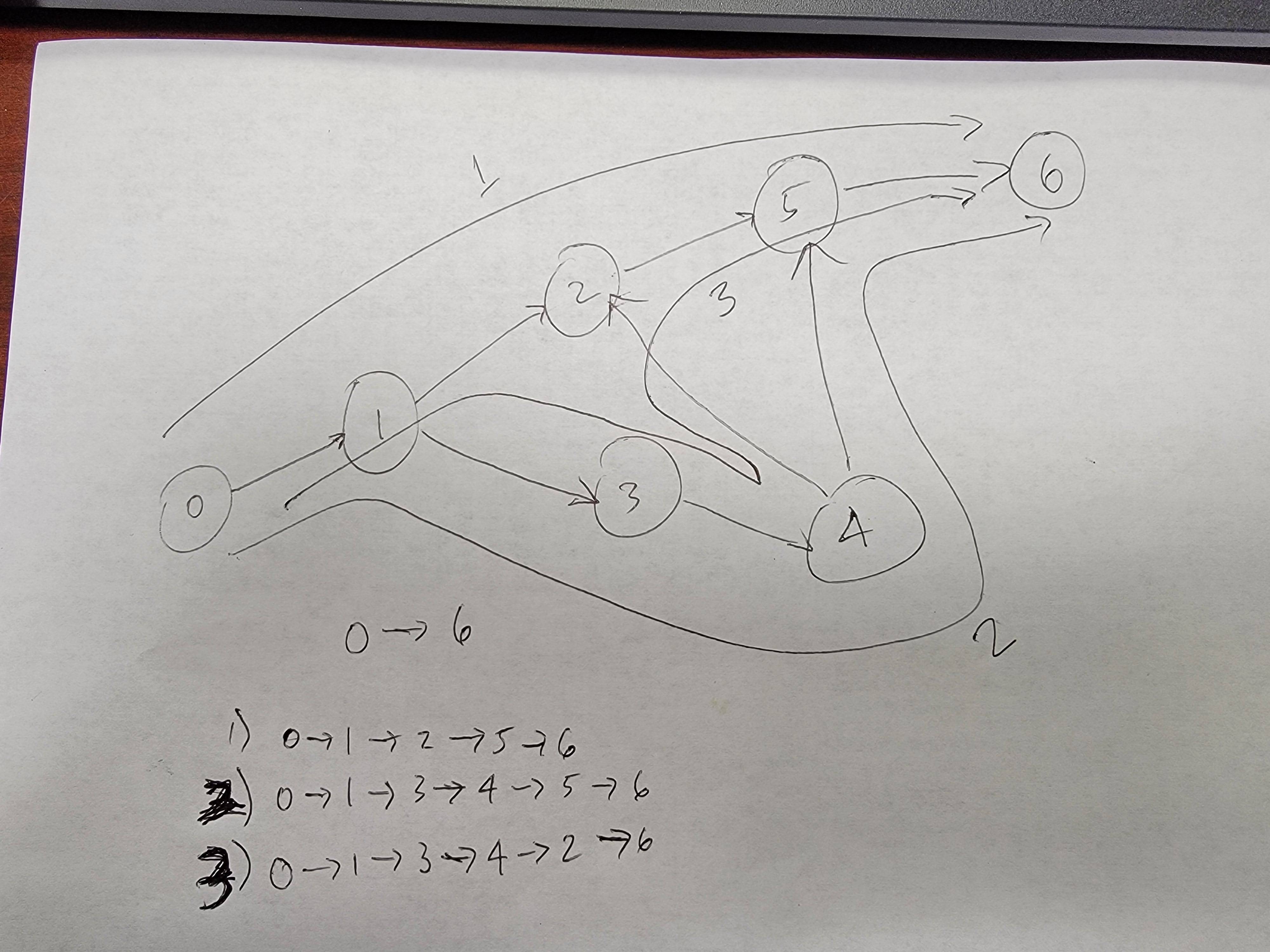
Here is the graph which i created :

g.addEdge(0, 1); 
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(2, 5);
g.addEdge(3, 4);
g.addEdge(4, 2);
g.addEdge(4, 5);
g.addEdge(5, 6);

I already compiled and run the program which start point is 0 and end point is 6. The result is 3, already looked up on YouTube about the algorithm but i still can't understand on how to visualize and how does the code flow on the recursion part inside a while loop.

CodePudding user response：

A recursive function must contain a base case to return a value rather than the result of the recursive call. In this case:

if(start > size || end > size || start < 0 || end < 0 || node == null)
{
    return;
}
    
if(visit[start]==true)
{
    return;
}

are those base cases that will break the recursive call chain. Remember, the method count_path returns void. If the method needed to return some value, you would've seen those if blocks returning some kind of default value. For instance, when you see examples of recursive Fibonacci, the base cases for Fib(0) and Fib(1) return the input value. Otherwise, it returns the result of the (cumulative) recursive call.

What are these base cases?

The method calculate the number of paths to some destination node from the current node. Therefore, if the node was already visited (and thus the paths should've been calculated already) simply return without recalculating. Also, if you have just one node in your graph, or no nodes, then there are no paths (so return without calculation).

Why is the answer 3 paths?

The picture below is based on the calls made to add edges. Each entry is a unidirectional path from a starting node to an ending node. So, starting at Node 0, to get to Node 6, there are three paths and they are outlined in the attached picture.

enter image description here