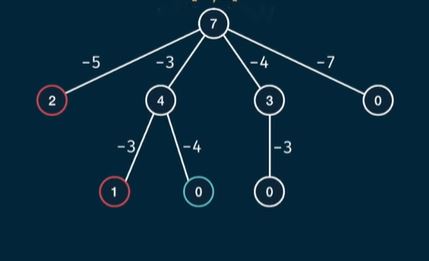
Just like the title says: The function to write has 2 parameters, the first is a number, the second a list of numbers:
example: (7, [5,3,4,7]) The Python function to write should return a list of numbers that when added would lead to '7' for example [3,4] or [4,3] or [7]
I wrote a Python function that actually works (see below bestSum()), but it only returns 1 working combination and I wish that someone could help edit it so it will return ALL possible "good" combinations. Then I could select the shortest one.
The recursive Python function is using a binary tree to go down by substracting a number from the list to the main number (substracting the same number is ok). If last node has 0 in it then that is a winner but if comes out as negative then that it is an impossible combination and should be dropped.
So instead of just returning, let say [4,3], it would return instead: ([3,4], [4,3], [7]) OR at least help me change the looping so it will not stop after it find the first working combination.
def bestSum(nb, intlist, res=[[], []]):
if (nb == 0):
res[0] = True
return res
if (nb < 0):
res[0] = False
return res
for i in intlist:
remainder = nb - i
res = bestSum(remainder, intlist, res)
if (res[0] == True):
res[1].append(i)
res[0] = True
return res
res[0] = False
return res
For now these 2 lines of code
res = bestSum(7, [5,3,4,7])
print("Shortest Result list is = ", res[1])
will return:
Shortest Result list is = [4, 3]
(Which is not really the shortest, it should be [7])
ATTENTION: This is NOT the same as the coin change problem since that coin problem also includes cents and always has a solution, and here we do not. So here there is not always a solution for example in the case of (7, [4,5]) there is no combination of 4 and 5 that can be added to lead to 7.
THANKS
CodePudding user response:
The underlying question is:
I have a recursive algorithm. When I make one or more recursive calls, I want to collect the results from those recursive calls, and use them to produce the result for this level of the recursion. (Simplest case: I want a list of all the recursive results.) How can I accomplish this simply?
It is much easier to reason about recursive algorithms when we don't rely on any side effects or mutable data structures. Modifying lists - especially when they are default parameters being used as a cache - quickly becomes a headache. Even if we get some immutable data back from the recursive calls (say, a tuple) and want to combine those results, it's often rather awkward. (It can be difficult to remember, for example, that some leaf result ought to be () or a singleton tuple, rather than None or a particular element value.)
The way around this, that I recommend, is to use a recursive generator instead. I wish to show several approaches, however, in order to explain some general technique for recursive algorithms.
Let's first consider the trivial example of listing all the nodes in a tree, in depth-first order:
def all_nodes_at(root):
# If this is a leaf node, then `root.children` is empty;
# so the loop will simply not run and nothing is yielded.
for child in root.children:
yield from all_nodes_at(child)
yield root # include the current node, after all nodes underneath.
# To see the results, we need to iterate over the generator in some way:
tree_nodes = list(all_nodes_at(tree_root))
Compare that to the approach using tuples:
def all_nodes_at(root):
result = ()
for child in root.children:
result = result all_nodes_at(child)
return result (root,)
tree_nodes = all_nodes_at(tree_root)
Seems considerably uglier to me. Using list caches:
def all_nodes_at(root, cache=[]):
for child in root.children:
cache.extend(all_nodes_at(child))
cache.append(root)
return cache
tree_nodes = all_nodes_at(tree_root)
Oof. Not only are we forced to return a value that we don't actually use in the recursion (so that we get a result at the top level), but it breaks if we want to use it more than once. "Oh, that's fine, we'll just clear the cache first." Really? You want to document that users need to do all_nodes_at.__defaults__[0].clear() before calling the function? Surely it would be better not to default the parameter. Better if it weren't a default parameter and the user supplied the initial cache:
def dump_all_nodes_at(root, cache):
for child in root.children:
cache.extend(all_nodes_at(child))
cache.append(root)
tree_nodes = []
dump_all_nodes_at(tree_root, tree_nodes)
At least this is reusable, and we don't have to play silly games with the return value (in fact, we don't have to return at all). But it's a really awkward interface now.
You can see why I generally prefer the recursive generator.
Let's apply the technique to the problem of finding all subsets with a given sum. But first, we need to think clearly about the recursive algorithm. We don't actually want, at a given step of the algorithm, to try each element. Why? Because if we only try the first element, then other elements will be handled by later steps in the recursion. Sure, that means we don't get every possible ordering of a given result set; but we can fix that later with e.g. itertools.permutations if it really matters. (Also, I'm pretty sure your approach doesn't prevent using the same element more than once.)
The simple definition is as follows: a subset with the given sum either includes the first element, or it does not. Our subsets consist of
- elements from the previous levels of the recursion that we decided to include;
- possibly the current element;
- elements from a recursive call on the remaining elements.
What we'll do is prepend the current element to results from the recursive call where appropriate (i.e., the one where we recursively called with a smaller target sum). The other elements will get automatically prepended as we bubble back through the recursion.
Thus:
def subsets_with_sum(values, target):
if target < 0:
# There are no solutions, so bail out.
return
if not values:
# Nesting the check like this allows for zeros in `values`.
if target == 0:
# We have reached the trivial solution.
yield ()
# No current element, therefore no more solutions.
return
# Otherwise, we recurse twice, yielding sub-results.
# First, some useful renaming
this_value, *other_values = values
for subset in subsets_with_sum(other_values, target - this_value):
yield (this_value,) subset # prepend and yield it back
# `yield from` is sugar for iterating and yielding each result directly.
yield from subsets_with_sum(other_values, target)
Let's test it:
>>> list(subsets_with_sum([5,4,3,7], 7))
[(4, 3), (7,)]
>>> list(subsets_with_sum(range(10), 10))
[(0, 1, 2, 3, 4), (0, 1, 2, 7), (0, 1, 3, 6), (0, 1, 4, 5), (0, 1, 9), (0, 2, 3, 5), (0, 2, 8), (0, 3, 7), (0, 4, 6), (1, 2, 3, 4), (1, 2, 7), (1, 3, 6), (1, 4, 5), (1, 9), (2, 3, 5), (2, 8), (3, 7), (4, 6)]
CodePudding user response:
Based on the comments in the question, we can pick the same element in the intlist multiple times to form a combination that sums up to the given target.
Iterative solution
Here we step through the different values in the intlist and build a new combination summing up to a given sum, and then adding new numbers in it.
def bestSum(target, intlist):
# initialize the dp dict
dp = {} # dp[combinationSum] = combination
for num in intlist:
dp[num] = [num]
# max steps we would need to arrive at a valid combination(if it exists) would be
# the combination containing only the min element in the intlist
# e.g. for target = 20 and intlist = [2,7], if we don't find a valid combination within
# 10 steps(all 2's), no valid answer would exist
for step in range(target//min(intlist) 1):
for combinationSum, combination in dp.copy().items(): # avoid modifying the dict while itrating
for i in intlist:
newSum = combinationSum i
if newSum == target:
# since we are taking a step one at a time, the first sum being equal to target
# will guarantee a shortest combination
return combination [i]
if newSum > target:
# skip if newSum if over target(skip adding additional entries into dp to improve perf)
continue
if not dp.get(newSum):
# if the dp already has an non-zero length list in it = its length is going to be
# at least equal to new combination length or lower, so we don't need to overwrite it
dp[newSum] = combination [i]
target, intlist = 20, [5,3,4,7]
print(bestSum(target, intlist))
prints
[5, 5, 5, 5]
for simplicity, here's what we would have in dp at each step for intlist = [5,3,4,7] and target of 20 -
Step : 0 - dp: {3: [3], 4: [4], 5: [5], 7: [7]}
Step : 1 - dp: {3: [3], 4: [4], 5: [5], 6: [3, 3], 7: [7], 8: [5, 3], 9: [5, 4], 10: [5, 5], 11: [4, 7], 12: [5, 7], 14: [7, 7]}
Step : 2 - dp: {3: [3], 4: [4], 5: [5], 6: [3, 3], 7: [7], 8: [5, 3], 9: [5, 4], 10: [5, 5], 11: [4, 7], 12: [5, 7], 13: [5, 5, 3], 14: [7, 7], 15: [5, 5, 5], 16: [5, 4, 7], 17: [5, 5, 7], 18: [4, 7, 7], 19: [5, 7, 7]}
Step : 3 - dp: {3: [3], 4: [4], 5: [5], 6: [3, 3], 7: [7], 8: [5, 3], 9: [5, 4], 10: [5, 5], 11: [4, 7], 12: [5, 7], 13: [5, 5, 3], 14: [7, 7], 15: [5, 5, 5], 16: [5, 4, 7], 17: [5, 5, 7], 18: [4, 7, 7], 19: [5, 7, 7], 20: [5, 5, 5, 5]}
Recursive Solution
If you want to stick with the recursive approach, you can make small changes to your original code to make it return all the combinations summing to the required target.
First of all, we don't need to make the function return True/False, instead we can just return None in case there is no valid combination that sums to the target value.
We want to collect all the combinations which sums to the required value so instead of returning the function on finding a valid combination what we should do is save it somewhere where we can access it later.
combinations = []
def bestSum(target, intlist, res=[]):
if (target == 0):
# found a valid combination
combinations.append(res) # collect the current combinations - THIS is what you were looking for
return
if (target < 0):
return
for i in intlist:
remainder = target - i
bestSum(remainder, intlist, res [i])
target, intlist = 20, [5, 4, 3, 7]
bestSum(target, intlist)
print(combinations, len(combinations))
now all your combinations which sum to the target are written to combinations now, but this has a few problems..
Above code prints -
[[5, 5, 5, 5], [5, 5, 4, 3, 3], [5, 5, 3, 4, 3], [5, 5, 3, 3, 4], [5, 5, 3, 7], [5, 5, 7, 3], [5, 4, 5, 3, 3], [5, 4, 4, 4, 3], [5, 4, 4, 3, 4], [5, 4, 4, 7], [5, 4, 3, 5, 3], [5, 4, 3, 4, 4], [5, 4, 3, 3, 5], [5, 4, 7, 4], [5, 3, 5, 4, 3], [5, 3, 5, 3, 4], [5, 3, 5, 7], [5, 3, 4, 5, 3], [5, 3, 4, 4, 4], [5, 3, 4, 3, 5], [5, 3, 3, 5, 4], [5, 3, 3, 4, 5], [5, 3, 3, 3, 3, 3], [5, 3, 7, 5], [5, 7, 5, 3], [5, 7, 4, 4], [5, 7, 3, 5], [4, 5, 5, 3, 3], [4, 5, 4, 4, 3], [4, 5, 4, 3, 4], [4, 5, 4, 7], [4, 5, 3, 5, 3], [4, 5, 3, 4, 4], [4, 5, 3, 3, 5], [4, 5, 7, 4], [4, 4, 5, 4, 3], [4, 4, 5, 3, 4], [4, 4, 5, 7], [4, 4, 4, 5, 3], [4, 4, 4, 4, 4], [4, 4, 4, 3, 5], [4, 4, 3, 5, 4], [4, 4, 3, 4, 5], [4, 4, 3, 3, 3, 3], [4, 4, 7, 5], [4, 3, 5, 5, 3], [4, 3, 5, 4, 4], [4, 3, 5, 3, 5], [4, 3, 4, 5, 4], [4, 3, 4, 4, 5], [4, 3, 4, 3, 3, 3], [4, 3, 3, 5, 5], [4, 3, 3, 4, 3, 3], [4, 3, 3, 3, 4, 3], [4, 3, 3, 3, 3, 4], [4, 3, 3, 3, 7], [4, 3, 3, 7, 3], [4, 3, 7, 3, 3], [4, 7, 5, 4], [4, 7, 4, 5], [4, 7, 3, 3, 3], [3, 5, 5, 4, 3], [3, 5, 5, 3, 4], [3, 5, 5, 7], [3, 5, 4, 5, 3], [3, 5, 4, 4, 4], [3, 5, 4, 3, 5], [3, 5, 3, 5, 4], [3, 5, 3, 4, 5], [3, 5, 3, 3, 3, 3], [3, 5, 7, 5], [3, 4, 5, 5, 3], [3, 4, 5, 4, 4], [3, 4, 5, 3, 5], [3, 4, 4, 5, 4], [3, 4, 4, 4, 5], [3, 4, 4, 3, 3, 3], [3, 4, 3, 5, 5], [3, 4, 3, 4, 3, 3], [3, 4, 3, 3, 4, 3], [3, 4, 3, 3, 3, 4], [3, 4, 3, 3, 7], [3, 4, 3, 7, 3], [3, 4, 7, 3, 3], [3, 3, 5, 5, 4], [3, 3, 5, 4, 5], [3, 3, 5, 3, 3, 3], [3, 3, 4, 5, 5], [3, 3, 4, 4, 3, 3], [3, 3, 4, 3, 4, 3], [3, 3, 4, 3, 3, 4], [3, 3, 4, 3, 7], [3, 3, 4, 7, 3], [3, 3, 3, 5, 3, 3], [3, 3, 3, 4, 4, 3], [3, 3, 3, 4, 3, 4], [3, 3, 3, 4, 7], [3, 3, 3, 3, 5, 3], [3, 3, 3, 3, 4, 4], [3, 3, 3, 3, 3, 5], [3, 3, 3, 7, 4], [3, 3, 7, 4, 3], [3, 3, 7, 3, 4], [3, 3, 7, 7], [3, 7, 5, 5], [3, 7, 4, 3, 3], [3, 7, 3, 4, 3], [3, 7, 3, 3, 4], [3, 7, 3, 7], [3, 7, 7, 3], [7, 5, 5, 3], [7, 5, 4, 4], [7, 5, 3, 5], [7, 4, 5, 4], [7, 4, 4, 5], [7, 4, 3, 3, 3], [7, 3, 5, 5], [7, 3, 4, 3, 3], [7, 3, 3, 4, 3], [7, 3, 3, 3, 4], [7, 3, 3, 7], [7, 3, 7, 3], [7, 7, 3, 3]] 123
A whopping 123 combinations just for a small target of 20. If you go through the list of combinations, you will notice that the combinations include all permutations of a given valid combination resulting in this bloated size. The code also has to do additional work to derive all those combinations.
What can we do to avoid these duplicates?
Sorting comes to the rescue; if we ensure that each valid combination is always sorted then there cannot be a permutation of the same combination in final combinations. How can this be leveraged in the code?
combinations = []
def bestSum(target, intlist, combination=[]):
if (target == 0):
# found a valid combination
combinations.append(combination)
return
if (target < 0):
return
for i in intlist[::-1]:
# each combination will be in ascending order
# while i is in descending order here, so if last element in my
# combination is greater than i, we can break the loop to stop
# additional work, and make sure that all the combinations are unique
if combination and combination[-1] > i:
break
remainder = target - i
bestSum(remainder, intlist, combination [i])
target, intlist = 20, [5, 4, 3, 7]
bestSum(target, sorted(intlist)) # sort list of values
print(combinations, len(combinations))
this outputs
[[5, 5, 5, 5], [4, 4, 5, 7], [4, 4, 4, 4, 4], [3, 5, 5, 7], [3, 4, 4, 4, 5], [3, 3, 7, 7], [3, 3, 4, 5, 5], [3, 3, 3, 4, 7], [3, 3, 3, 3, 4, 4], [3, 3, 3, 3, 3, 5]] 10
Now, we don't have any permutations in our combinations! And we can easily get all the shortest/longest combinations as needed from the combinations.
But as pointed out by @karl in his answer, the interface for this looks quite bad, and we should actually use recursive generators to make the interface cleaner. Which would look something like this -
def bestSum(target, intlist, combination=[]):
if (target == 0):
# found a valid combination
yield combination
if (target < 0):
return
for i in intlist[::-1]:
if combination and combination[-1] > i:
break
remainder = target - i
yield from bestSum(remainder, intlist, combination [i])
target, intlist = 20, [5, 4, 3, 7]
intlist.sort()
targetCombinations = list(bestSum(target, intlist))
targetCombinations.sort(key=lambda x: len(x))
print("One of the shortest combination - ", targetCombinations[0])
I would still recommend the iterative solution over the recursive solution above because given a intlist of size n, the tree you have in your diagram would be an n-ary tree, having n branches on each node starting from target at the top. The iterative solution would be similar to a level order traversal in the n-ary tree and would stop when it reaches the level where it finds the solution. While the recursive solution would be DFS over the tree and it would need to go through each and every combinations(pruning duplicate permutations) of the n-ary tree.
CodePudding user response:
This is a simple one :
import itertools as it
# create all possible route
def create_permutation(data):
final = []
for k in range(1, len(data) 1):
temp = list(it.permutations(data, k))
final.extend(temp)
return final
# find best sum in equal to num
def best_sum(subs, num, _min = True):
final = []
for i in range(len(subs)):
temp_sums = sum(subs[i])
if temp_sums == num:
final.append(subs[i])
if not final:
return None
# if only wants minimum then sort by length then return first
if _min:
return sorted(final, key = lambda x : len(x))[0]
return final
def main(data, num):
subs = create_permutation(data)
result = best_sum(subs, num, False)
print("Best === ", result)
data = [5, 3, 4, 7, 2]
num = 7
main(data, num)