How do I find Point3 Position by we know Point1 and Point2 Position and length of Line Point1 to Poi-CodePudding

I need a formula to calculate the position of the third point, by we knowing that the position of the Point1 and Point2 and the length of the line (Point1, Point2) and the length of the line (Point1, Point3).

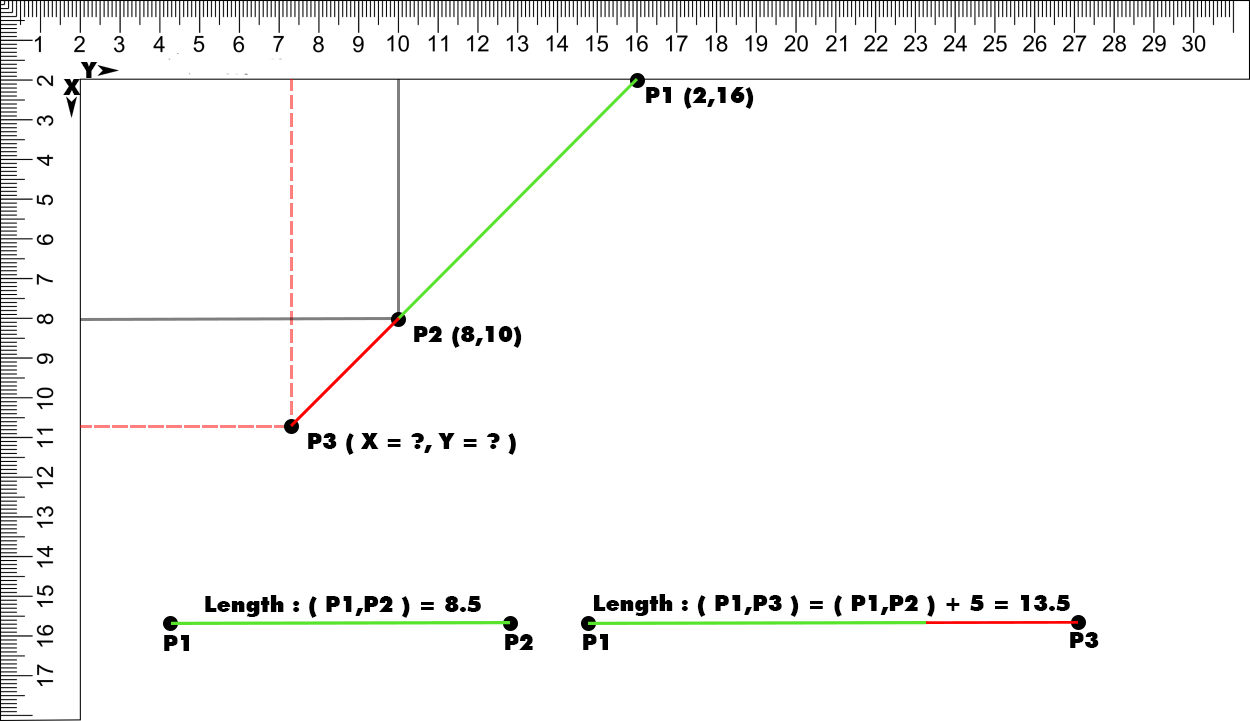
>>>> this is a picture of this question <<<<

# We represent it as follows:

Point1 as P1, Point2 as P2, Point3 as P3
P1 = (2, 16) or P1x,P1y = (2, 16)
P2 = (8, 10) or P2x,P2y = (8, 10)

length of the line (P1, P2) as L1, Length of the line (P1, P3) as L2
# I want to make length of the L2 longer than L1 ( so I plus 5 to length of the line L1 )
L1 = 8.5
L2 = L1   5 = 13.5 

Find : Point 3 => P3 = (P3x = ?, P3y =?)

This is my code: how I find the length of the line.

import math
def calculateDistance(x1,y1,x2,y2):
    dist = math.sqrt((x2 - x1)**2   (y2 - y1)**2)
    return dist

So How we can find position of P3?

Find : P3 = (P3x = ?, P3y =?)

CodePudding user response：

Vectors P1->P3 and P1->P2 are collinear, which means the coordinates of P1->P3 are proportional to the coordinates of P1->P2; and the proportionality factor must be exactly the ratio of lengths length(P1->P3) / length(P1->P2).

This gives you an equation for P3x and P3y:

P3x - P1x == (L2 / L1) * (P2x - P1x)
P3y - P1y == (L2 / L1) * (P2y - P1y)

Turning this into a definition for P3x and P3y:

ratio = L2 / L2
P3x = P1x   ratio * (P2x - P1x)
P3y = P1y   ratio * (P2y - P1y)

Note that you don't need to define your own distance function; there is already one in the standard library math module: https://docs.python.org/3/library/math.html#math.dist

from math import dist

print( dist((2,16), (8,10)) )
# 8.485281374238571