In ghci:
:t (*)
(*) :: Num a => a -> a -> a
:t (/)
(/) :: Fractional a => a -> a -> a
Why does division require fractional inputs?
I mean, I understand 'why' (because it was written to do so), but I don't understand why it was implemented this way? * can take and return fractionals, why can't / ? I know that div and quot exist, but I don't see why / wouldn't convert it's arguments like * seems to (or why it wouldn't just become an alias for div/quot depending on the given arguments.
I'm sure there is a reason, I just can't figure out what it is?
CodePudding user response:
I think you might be confused about what the constraints mean. There is no automatic conversion going on in either of these operations. The constraint is essentially a set of types which support this operation. Num is the most basic numeric class, and its members include Integer, Double, Rational, etc., which means that (*) can have any of the following types:
(*) :: Integer -> Integer -> Integer
(*) :: Double -> Double -> Double
(*) :: Rational -> Rational -> Rational
Notice especially that all three types are the same -- you have to put in two of the same type, and you always get back what you put in.
You cannot divide two integers and get back an integer in general, so we must not allow
(/) :: Integer -> Integer -> Integer
and that is why there is the more specific class Fractional for numeric types which are closed under division.
It would be possible to make (/) an alias for div in the integer case, as you suggest. In fact, it is possible––you could just write this in your source file:
instance Fractional Integer where
(/) = div
fromRational = floor
Now Integers support the (/) operator for integer division, just like every other language! I recommend strongly against this, I think the Haskell language designers got this one right. Putting aside the total insanity of allowing you to write the literal 0.5 in an integer context and have it silently interpreted as zero instead of an error (which a worrying number of languages allow!), integer division is a very different operation than division. Division is the inverse of multiplication, and it has these nice laws:
(a / b) * b = a
(a b) / c = (a / c) (b / c)
(IEEE rounding errors notwithstanding), integer division is not and does not. So if (/) supported integers, then if you had some polymorphic arithmetic function:
someFormula x y = x / (x^2 y^2) y / (x^2 y^2)
and you're like, hey, that is unnecessarily complicated, let me simplify it!
someFormula x y = (x y) / (x^2 y^2)
You have just introduced a bug for that user who decided to use someFormula on integers, for which it was never intended, because in that case division was not "real" division (no pun intended), and your algebra was wrong. So that's why we have Fractional to indicate that this is an honest type supporting division, that is to say, the inverse of multiplication.
CodePudding user response:
(*) :: Num a => a -> a -> a means you can pick any type a you like that is a member of Num, and * can be a function that takes two arguments of that type and returns a result of the same type.
The way type classes work, for each type that is a member of Num a separate implementation of * must be supplied. So there is one function that is (*) :: Integer -> Integer -> Integer, another that is Double -> Double -> Double, another that is Ratio Word32 -> Ratio Word32 -> Ratio Word32, etc, etc. * can be instantiated as any of those separate functions.
Similarly, (/) :: Fractional a => a -> a -> a means you can pick any type a, but here it has to be a member of the Fractional type class, which is more restrictive. Double is a member of Fractional, so there is a (/) :: Double -> Double -> Double function. Integer is just not a member of Fractional, so there is no (/) :: Integer -> Integer -> Integer function.
The reason Integer is not a member of Fractional is that mathematical division of integers simply doesn't result in an integer. You need a type that supports fractional numbers between the integers in order for division to make much sense. There are different operations like div and quot that you can perform on integers, and so they work on types like Integer and Int. If you want one of those operations, you should ask for it, not ask for / and expect it to give you a different operation when you use it on integers. Not least because how would it know whether div or quot is what you think of as "the closest thing to division I can do with integers"? And if you have an Int, Integer, or similar, and you want to translate it to a fractional number so you can do division with it and get a fractional result, then you'll need to use a translation function like fromIntegral; Haskell will not magically insert this for you, but it has all the translation functions and they work just fine.
Note that there is no conversion going on when you call *; it is not that * is happy to convert argument in ways that / is not. The Int version of * requires that you provide it with two Int arguments, the Double version requires that you provide it with two Double arguments, etc. If you call the Double version of * but pass it an Int, it will not convert the Int to a Double: you will get a type error.
New Haskellers often think there must be conversion because they can evaluate expressions like 3.2 * 7, and how else could that work?
In several other popular languages what happens here is that the language implementation says that 3.2 is a floating point number and 7 is an integer, and - like in Haskell - multiplication can only be evaluated with two arguments of the same type. So the language implementation silently inserts some code to translate the integer to the floating point type; what you get is actually something like 3.2 * (floatFromInt 7). But just because that is how other languages handle simple arithmetic expressions doesn't make it the only way, and you would do very well to find out how Haskell (or any other language you start learning) actually handles these expressions when you start learning the language rather than assuming it must be like it is any other language.
In Haskell, the compiler doesn't start by assuming numeric literals like 3.2 or 7 are any particular type. Haskell is more flexible. Instead any integer-like number in the source code can be read as a literal for any numeric type (any type in Num), while a decimal-point number in the source code can be read as a literal for any type in Fractional. Haskell figures out what what version of * is being called by looking at both the context it is used in (the code that consumes the result) as well as the arguments. If any one of those things forces a single type, then both arguments as well as the result must be able to be that single type.
So in cases like 3.2 * 7 it is likely that how the result is used will determine what type the result must be, which in turn determines what the type of * is in that expression, which in turn determines how each of the numeric literals are read. Both will be read in as literals for that same type1. In this case we can even determine that 7 is definitely not Int, or Integer, or anything similar, since those types do not have Fractional instances and the type used must be a Fractional one in order for one of the arguments to use a 3.2 literal containing a decimal point.
1. Of course what "being read in as a literal for any numeric type" actually means is that an integer literal makes Haskell create an Integer and then the fromInteger :: Num a => Integer -> a function from the appropriate type's Num instance can build the "real" value from the Integer. Similarly the decimal-point literals are initially read as a value of type Rational and then the fromRational :: Fractional a => Rational -> a function is used to build the real value.
So if you're being very picky and/or technical, you can argue that 3.2 is in fact always a literal for the fixed type Rational and then the conversion function fromRational is always applied. That is not incorrect, but I view it as an implementation strategy for the concept "3.2 is a literal for any Fractional type". The application of the function will almost always be inlined away at compile time anyway, so at runtime there will only be the values of the final desired type.
I think this point of view is more helpful for new Haskellers precisely because so many get confused expecting automatic type conversion between integers and floating point types to happen as they do in other languages, and that most definitely is not the case; in those other languages that would happen with variables of integral types as well. This form of conversion that Haskell has is only to do with literals, and it's rather different because the fromRational (or fromInteger) translator is always called when you use a literal, it has nothing to do with promoting a real runtime value of one type to match the type of another operand.
CodePudding user response:
In these types:
:t (*)
(*) :: Num a => a -> a -> a
:t (/)
(/) :: Fractional a => a -> a -> a
There are two parts:
- Constraints :Num, Fractional
- Types: a
The a part means 'any type' you want (subject to the constraints), but it's the same type in every place because it has a in every place. Also, please note that no conversion is taking place, precisely because the type is a in every place. The Num and Fractional part is the 'superclass' in the type hierarchy:
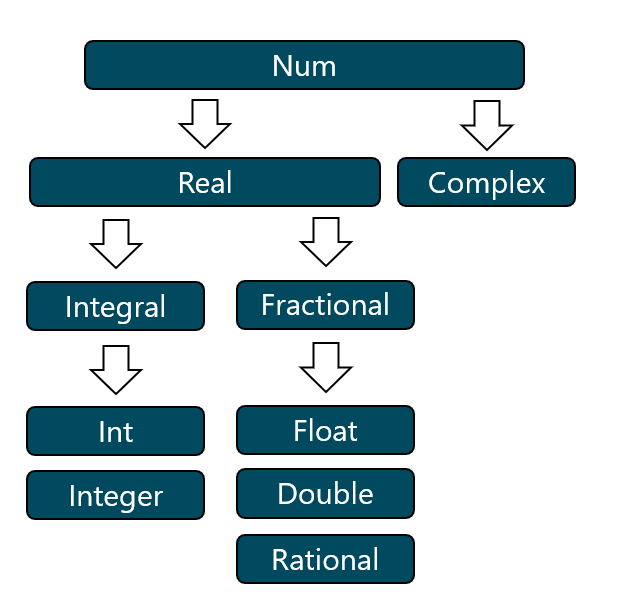
So, Num a means Real, or Complex, or Integral, or Int, or Integer, or Fractional , or Float, or Double, or Rational.
The thing is that mathematically integral division is different from fractional division. Thus, Haskell has div for integral division, and / for fractional division.
:t div
div :: Integral a => a -> a -> a
:t (/)
(/) :: Fractional a => a -> a -> a
One of the consequences is that you have to think very carefully about your algorithm. Take for example, calculating the average of the values in a list:
average xs = (sum xs) / length (xs)
Simple, but wrong. This will not compile, because the types are wrong:
:t sum
sum :: (Foldable t, Num a) => t a -> a
:t length
length :: Foldable t => t a -> Int
So, you have to use Data.List's genericLength.
:t genericLength
genericLength :: Num i => [a] -> i
average :: Fractional a => [a] -> a
average xs = (sum xs) / genericLength (xs)