#include <cstdlib>
#include <iomanip>
#include <iostream>
using namespace std;
const int n = 5;
void fill_matrix(int (*matrix)[n])
{
    for (int row = 0; row < n; row  )
    {
        for (int col = 0; col < n; col  )
            matrix[row][col] = rand() % 201 - 100;
    }

}

void print_matrix(int (*matrix)[n])
{
    for (int row = 0; row < n; row  )
    {
        for (int col = 0; col < n; col  )
            cout << setw(4) << matrix[row][col];
        cout << std::endl;
    }
}

int main()
{
    int matrix[n][n];
    int sum = 0;
    fill_matrix(matrix);
    print_matrix(matrix);

    for (int row = 0; row < n; row  )
    {
        for (int col = 0; col < n; col  )
        {
        }
    }
    return 0;
}

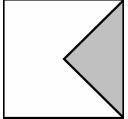
I can't realize how I can loop over this part of the matrix. The matrix can be a different size. So I can't imagine an algorithm to get the right triangle of the matrix

CodePudding user response：

It is important to realise, that the widest point of the triangle is at its tip.

Let i = 1 So going from the top row to the bottom, do:

Start:

• set the last i fields in this row to 1.

• if i is smaller than the height of the matrix, increase i by one

• else if it is greater than the height, decrease it by one

Go back to start

CodePudding user response：

Consider the generic nested loops used in the posted code to traverse the "matrix", just written in a slightly different way.

for (int row = 0; row < n; row  )
{
    int const first_col = 0;
    int const last_col = n;
    for (int col = first_col; col < last_col; col  )
    {
        // ...
    }
}

At the right side of the greyed area in OP's posted image, every row terminates at the boundary of the matrix (so that we don't really need a last_col variable, the original condition is fine).

Note, though, that all the matrix elements inside this area are at the right (or on) of both the leading diagonal and the antidiagonal.

Now, what would be the mathematical equation of the leading diagonal, given the row?

column = f(row) = row

What about the antidiagonal? Look at its definition (from Wolfram):

An antidiagonal is defined as a list of elements for which the sum of the indices are equal, where the first element is in the top-right of a matrix

So, given a matrix of size n x n and remembering that in C array indices are 0-based, we can say:

column = g(row) = n - 1 - row

As already noted, the value we need to initialize first_col in the outer loop is the max of these two values.