Python Generate Random Numbers with n standard deviations of a mean-CodePudding

I am dealing with numeric ranges obtained from a normal population that represent - 2 standard deviations from the mean. Abnormal values are those that extend out past the 2SD limits. I want to generate random values that are skewed to look like the population data. So that I provide a mean and the -2SD range to a function that generates numbers that produce a perfect bell curve that looks like the original population. So for example, take a lab test like glucose with a reference range of 60 - 100. This represents the values that would be obtained by testing a large group of normal people. The mean is 80 and the 2SD range is 60-100. That is 95% of the total population by definition. Values can extend out from below 50 upwards to 500. I would like to generate random numbers that fit these parameters.

I am playing with numpy and scipy but I don't understand the math very well. Is there a function that will do this?

CodePudding user response：

np.random.normal does that. The first parameter is the means, the second is the standard deviation (SD) and the third is the number of samples to generate. In your case, the means is 80 and the SD is 10. Thus, you can use the following code to generate 1_000_000 items:

import numpy as np
arr = np.random.normal(80, 10, 1_000_000)

To check the result is statistically correct you can use:

# Example of result: 0.954208 (ie. 95.4% are in the 60-100 range)
((arr > 60) & (arr < 100)).sum() / arr.size

CodePudding user response：

The built-in random module can generate numbers in a normal distribution. normalvariate() takes the mean and standard deviation:

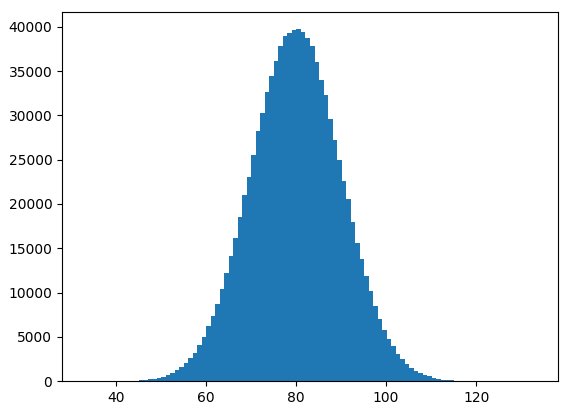
import random
from matplotlib import pyplot as plt

plt.hist([random.normalvariate(80, 10) for _ in range(1_000_000)], bins=100)
plt.show()

Output:

matplotlib normal distribution