I have this dataset and I am trying to fit a model that assesses whether treatment has an impact on weight (outcome) and in particular, that allows the treatment effect to vary over time. There are multiple measurements per 'id'.
I am trying to analyze the data using a repeated measures ANOVA. The dataset contains a few variables: id (the patient’s unique identifier), treatment (an indicator for whether the patient received the new diet (1) or not (0)), and age (the patient’s age in years at study entry), outcome (the patient’s weight in pounds recorded at a particular visit), and visitnumber (the visit number).
> dput(full)
structure(list(id = c(965, 168, 133, 566, 145, 79, 49, 182, 998,
476, 314, 578, 800, 712, 574, 858, 743, 260, 155, 493, 411, 397,
232, 972, 357, 27, 794, 39, 723, 711, 982, 305, 804, 504, 607,
146, 168, 890, 720, 170, 379, 841, 543, 825, 771, 224, 8, 739,
876, 844, 5, 308, 997, 275, 802, 552, 683, 488, 743, 61, 439,
687, 172, 990, 101, 979, 57, 498, 148, 694, 810, 970, 470, 442,
321, 650, 22, 735, 622, 697, 601, 845, 689, 783, 297, 502, 901,
902, 907, 933, 831, 848, 238, 244, 562, 238, 54, 307, 157, 833
), outcome = c(178.1292789, 152.6929382, 154.9682105, 180.1792337,
155.5643838, 158.1777561, 141.2326605, 158.0372637, 170.7657935,
150.0930737, 144.8978423, 167.7295463, 170.4530778, 166.2320969,
174.6196961, 172.9699754, 165.6665897, 143.5506991, 150.8801473,
152.8867248, 141.627696, 147.7234166, 144.2490439, 186.4303623,
137.4472087, 150.8790336, 175.1623773, 156.37109, 177.8236086,
170.4165886, 175.8410723, 143.3243023, 159.6941819, 180.1754229,
163.2772414, 143.8418165, 143.5552981, 172.6175974, 177.6680813,
137.9041874, 163.4326879, 178.2426015, 173.1707072, 176.0714329,
165.7867407, 145.6877951, 150.2737186, 184.4544812, 158.2952331,
182.1838354, 148.9614953, 149.8798918, 156.5142777, 163.2968075,
177.3107927, 165.4462144, 167.9021459, 148.1217567, 163.2306892,
145.5216289, 154.5574847, 179.0495321, 145.9386308, 181.1654107,
144.8315221, 171.6145523, 148.5750191, 144.775874, 148.1463073,
172.590192, 160.9216146, 174.7643147, 139.3596933, 157.1786811,
153.3880836, 183.8471692, 148.5695133, 173.8687851, 151.5755017,
165.0664097, 180.3950209, 164.5429984, 164.983456, 178.9630521,
137.9087173, 168.668939, 169.8311543, 180.9404174, 174.0725322,
173.8267465, 174.4805713, 166.6538422, 137.5949582, 152.1977455,
166.0765327, 148.9605142, 140.4552133, 147.5073477, 146.426167,
164.9396603), visitnumber = c(4, 3, 1, 4, 1, 2, 2, 1, 2, 2, 5,
2, 5, 1, 4, 2, 2, 5, 3, 3, 4, 4, 1, 5, 5, 4, 4, 3, 4, 4, 1, 2,
2, 5, 1, 5, 5, 4, 5, 5, 1, 5, 3, 2, 1, 3, 3, 5, 1, 5, 4, 4, 1,
2, 5, 3, 1, 1, 1, 4, 3, 5, 4, 4, 4, 1, 5, 3, 3, 2, 2, 5, 4, 2,
2, 4, 3, 1, 1, 2, 2, 2, 2, 5, 3, 2, 5, 4, 2, 5, 4, 1, 5, 1, 2,
2, 4, 2, 3, 1), treatment = c(0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1,
0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0,
1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1,
1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0,
1, 1, 1, 1, 0), age = c(62.56849707, 59.9875489, 58.92425704,
62.86864989, 55.61336473, 64.98774785, 61.58430531, 66.91110054,
60.15734064, 61.336864, 56.22408195, 57.41464728, 62.32706193,
56.24078384, 59.9129205, 59.72669943, 60.7366701, 68.07162556,
65.83706817, 58.34790981, 62.92541931, 60.44772228, 59.05602316,
60.3587956, 64.20115418, 53.6724036, 63.85708009, 56.08114237,
65.0820994, 58.23011895, 62.12986331, 61.85220756, 54.94833195,
54.9549317, 59.08634974, 66.85477235, 59.9875489, 57.57695066,
54.79087254, 66.9157855, 66.20755394, 59.35629854, 62.46671274,
67.65557345, 61.17523285, 60.83744515, 55.4094255, 61.50789629,
60.07359108, 55.77166234, 66.2290783, 56.01880637, 65.75930218,
64.63645494, 59.35355296, 62.6060523, 70.28167557, 52.91174325,
60.7366701, 57.8139364, 58.41752334, 56.53555588, 58.75351312,
60.74961013, 61.51029989, 54.9842095, 56.00229494, 64.40211717,
54.86495493, 66.54053274, 53.74773261, 62.06325335, 59.65814464,
59.07963141, 59.17691183, 53.61106941, 62.58076922, 67.01218874,
54.08783732, 61.38234868, 61.70638178, 61.59147749, 62.97231388,
64.1034271, 53.7801112, 62.22005378, 61.43731322, 60.49405197,
62.2994082, 56.56848077, 59.85286766, 61.65844302, 59.36361724,
61.53807386, 62.97919029, 59.36361724, 61.85642462, 59.21186756,
56.24220335, 61.16389981)), row.names = c(4336L, 750L, 596L,
2524L, 648L, 353L, 211L, 811L, 4487L, 2132L, 1409L, 2577L, 3587L,
3184L, 2559L, 3854L, 3325L, 1158L, 691L, 2204L, 1842L, 1781L,
1032L, 4368L, 1602L, 117L, 3558L, 169L, 3237L, 3182L, 4411L,
1366L, 3602L, 2256L, 2708L, 656L, 752L, 3997L, 3224L, 760L, 1699L,
3779L, 2427L, 3700L, 3452L, 999L, 35L, 3309L, 3930L, 3794L, 22L,
1382L, 4481L, 1228L, 3596L, 2466L, 3051L, 2184L, 3324L, 268L,
1966L, 3073L, 769L, 4450L, 454L, 4396L, 251L, 2227L, 661L, 3104L,
3629L, 4359L, 2105L, 1978L, 1440L, 2905L, 96L, 3289L, 2774L,
3119L, 2682L, 3796L, 3080L, 3509L, 1330L, 2244L, 4045L, 4049L,
4070L, 4190L, 3732L, 3808L, 1063L, 1088L, 2504L, 1060L, 235L,
1375L, 700L, 3739L), class = "data.frame")
I did model <- aov(outcome~factor(treatment) Error(factor(id)), data = new) but not sure this is correct.
Many thanks!
CodePudding user response:
You can run a one way repeated measures ANOVA model as follows, assuming that visitnumber is the only within-subject factor, to examine whether treatment has an effect on the weight outcome across the five visits (I defined sample data as df):
rm_model <- aov(outcome ~ treatment age Error(id/visitnumber), data = df)
summary(rm_model)
# > summary(rm_model)
#
# Error: id
# Df Sum Sq Mean Sq
# treatment 1 11053 11053
#
# Error: id:visitnumber
# Df Sum Sq Mean Sq
# treatment 1 813.4 813.4
#
# Error: Within
# Df Sum Sq Mean Sq F value Pr(>F)
# treatment 1 2759 2759.4 64.97 2.24e-12 ***
# age 1 21 21.2 0.50 0.481
# Residuals 95 4035 42.5
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
CodePudding user response:
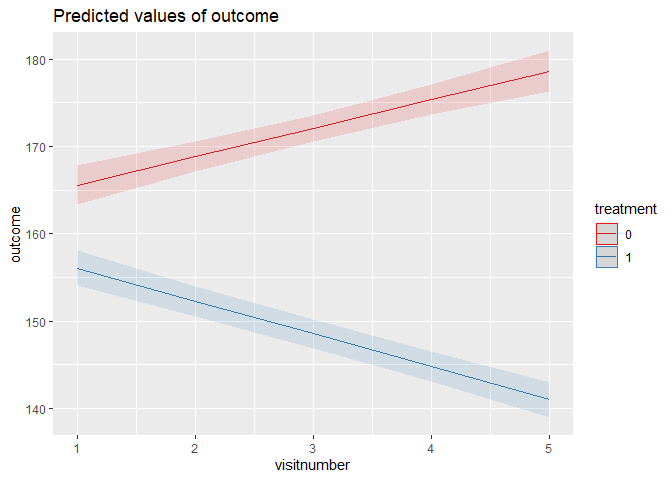
You can run a mixed effects model using lme4(). You would include random intercepts for id, and can include a treatment by visitnumber interaction to allow the effect of treatment to vary over time.
library(lme4)
library(sjPlot)
model_linear <- lmer(
outcome ~ treatment * visitnumber (1 | id), # random intercepts for id
data = mydata
)
summary(model_linear)
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: outcome ~ treatment * visitnumber (1 | id)
#> Data: mydata
#>
#> REML criterion at convergence: 607.8
#>
#> Scaled residuals:
#> Min 1Q Median 3Q Max
#> -0.85534 -0.11282 0.00127 0.12433 0.95700
#>
#> Random effects:
#> Groups Name Variance Std.Dev.
#> id (Intercept) 28.9641 5.3818
#> Residual 0.7958 0.8921
#> Number of obs: 100, groups: id, 97
#>
#> Fixed effects:
#> Estimate Std. Error t value
#> (Intercept) 162.3155 1.5297 106.111
#> treatment -2.4956 1.9717 -1.266
#> visitnumber 3.2594 0.4517 7.216
#> treatment:visitnumber -7.0199 0.5466 -12.844
#>
#> Correlation of Fixed Effects:
#> (Intr) trtmnt vstnmb
#> treatment -0.776
#> visitnumber -0.872 0.676
#> trtmnt:vstn 0.721 -0.826 -0.826
plot_model(model_linear, terms = c("visitnumber", "treatment"), type = "pred")
# add quadratic term for time
model_quadratic <- lmer(
outcome ~ treatment * poly(visitnumber, 2) (1 | id),
data = mydata
)
summary(model_quadratic)
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: outcome ~ treatment * poly(visitnumber, 2) (1 | id)
#> Data: mydata
#>
#> REML criterion at convergence: 582.7
#>
#> Scaled residuals:
#> Min 1Q Median 3Q Max
#> -2.140e-03 -2.970e-04 7.930e-06 3.135e-04 2.350e-03
#>
#> Random effects:
#> Groups Name Variance Std.Dev.
#> id (Intercept) 2.985e 01 5.463718
#> Residual 4.837e-06 0.002199
#> Number of obs: 100, groups: id, 97
#>
#> Fixed effects:
#> Estimate Std. Error t value
#> (Intercept) 171.9800 0.7511 228.961
#> treatment -23.7468 1.1147 -21.302
#> poly(visitnumber, 2)1 46.1923 6.6151 6.983
#> poly(visitnumber, 2)2 4.0663 2.4504 1.659
#> treatment:poly(visitnumber, 2)1 -90.0634 6.6152 -13.615
#> treatment:poly(visitnumber, 2)2 -16.7434 2.4506 -6.832
#>
#> Correlation of Fixed Effects:
#> (Intr) trtmnt p(,2)1 p(,2)2 t:(,2)1
#> treatment -0.674
#> ply(vst,2)1 -0.041 0.028
#> ply(vst,2)2 -0.041 0.028 1.000
#> trtmn:(,2)1 0.041 -0.028 -1.000 -1.000
#> trtmn:(,2)2 0.041 -0.028 -1.000 -1.000 1.000
plot_model(model_quadratic, terms = c("visitnumber", "treatment"), type = "pred")
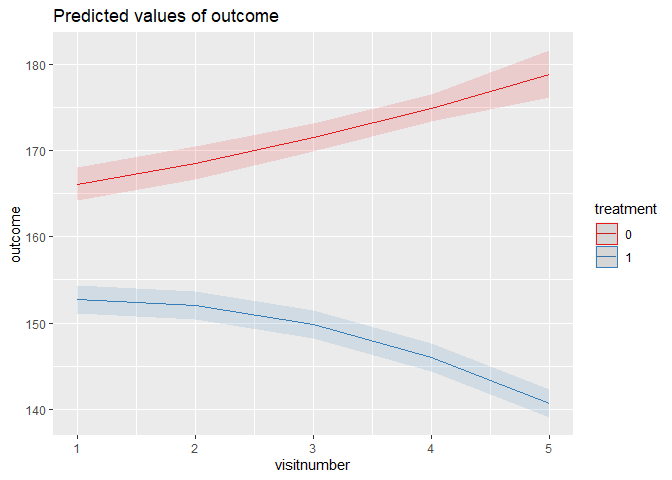
Created on 2022-03-14 by the reprex package (v2.0.1)
