I ran a propensity matching to test the effect of a medical treatment. I want to compare the demographics of the control group with the treatment group. How do I create a basic table to compare them?
this is my code so far
#defining variables
Tr <- cbind(VAECMO)
Y <- cbind (DIED)
X <- cbind(AGE, RACE, CKD, RSPTFL, ZIPINC_QRTL, CLUNGD)
#descriptive statistics
summary(Tr)
summary(Y)
summary(X)
#Propensity score model
glm1 <- glm(Tr ~ X, family = binomial, data = comor)
summary(glm1)
#making sure there are no missing values in the necessary observations
length(Tr)
length(glm1$fitted)
#Average Treatment on the treated effect
rr1 <- Match(Y = Y, Tr = Tr, X = glm1$fitted)
summary(rr1)
I want to create a table that compares the average age, composition of race, etc of those who received the Tr and those who didn't.
CodePudding user response:
What you want is to check the balancing you achieved with PS matching, i.e., whether the descriptives of the treated and the control have reasonably converged.
Matching::MatchBalance provides a rich set of comparative statistics, which helps to draw the respective conclusions.
Here an example using the lalonde data. Note, that you shouldn't apply one-to-one matching when using propensity scores, i.e. the number of matches should not be one, use e.g. M=5. Also a caliper= of e.g. 0.25 standard deviations of maximal acceptable distance for matches should be used to take some account of the common support in both groups.
library(Matching)
data(lalonde)
## Estimate propensity score
fit <- glm(treat ~ age I(age^2) educ I(educ^2) black
hisp married nodegr re74 I(re74^2) re75 I(re75^2)
u74 u75, family=binomial, data=lalonde)
lalonde$ps <- fit$fitted.values ## store ps in data set
## matching
rr <- with(lalonde, Match(Y=re78, Tr=treat, X=ps, M=5, caliper=.25))
To compare the groups, define a set of comparison variables to easily subset later.
## define comparison variables
(comp <- c('ps', all.vars(fit$call)[1:11]))
# [1] "ps" "treat" "age" "educ" "black" "hisp" "married"
# [8] "nodegr" "re74" "re75" "u74" "u75"
To just compare the groups without any matching, simply aggregate the mean or something else.
aggregate(. ~ treat, lalonde[comp], mean)
# treat ps age educ black hisp married nodegr re74 re75 u74 u75
# 1 0 0.3936490 25.05385 10.08846 0.8269231 0.10769231 0.1538462 0.8346154 2107.027 1266.909 0.7500000 0.6846154
# 2 1 0.4467636 25.81622 10.34595 0.8432432 0.05945946 0.1891892 0.7081081 2095.574 1532.056 0.7081081 0.6000000
To compare the groups before and after matching use Matching::MatchBalance. You may easily use reformulate in the function's formula interface. For the before-after comparison, provide your result rr in match.out=. (To omit console output, use print.level=0.)
bal <- MatchBalance(formul=reformulate(comp[-2], 'treat'), data=lalonde,
match.out=rr)
# ***** (V1) ps *****
# Before Matching After Matching
# mean treatment........ 0.44676 0.43271
# mean control.......... 0.39365 0.4327
# std mean diff......... 45.329 0.010439
#
# mean raw eQQ diff..... 0.054029 0.0017398
# med raw eQQ diff..... 0.060548 0.00085473
# max raw eQQ diff..... 0.10393 0.024826
#
# mean eCDF diff........ 0.13402 0.0043977
# med eCDF diff........ 0.15743 0.0032538
# max eCDF diff........ 0.22443 0.029284
#
# var ratio (Tr/Co)..... 1.2101 0.99967
# T-test p-value........ 1.4842e-06 0.97518
# KS Bootstrap p-value.. < 2.22e-16 0.782
# KS Naive p-value...... 3.7341e-05 0.82407
# KS Statistic.......... 0.22443 0.029284
#
# [...]
#
# Before Matching Minimum p.value: < 2.22e-16
# Variable Name(s): ps Number(s): 1
#
# After Matching Minimum p.value: 0.02
# Variable Name(s): re75 Number(s): 9
Basically, for each variable the function compares the treatment groups before and after matching; mean and standardized mean differences are provided as well as p-values of t-tests and KS tests. At the very bottom, the output states the worst variables according to the t-test p-values.
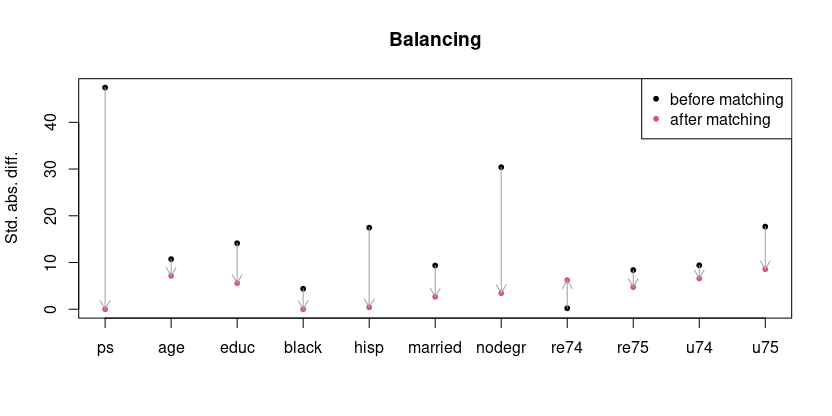
However, rather than t-tests, in the literature commonly provided are the standardized absolute differences, which in the ideal case should of course be close to zero and may be extracted from the balancing like so:
(sad <- cbind(sapply(bal$BeforeMatching, '[[', 'sdiff.pooled'),
sapply(bal$AfterMatching, '[[', 'sdiff.pooled')) |>
abs() |>
`dimnames<-`(list(comp[-2], c('before', 'after'))))
# ps 47.4345458 0.0104392
# age 10.7277121 7.1516980
# educ 14.1219821 5.5883637
# black 4.3886611 0.0177414
# hisp 17.4561071 0.4161040
# married 9.3640701 2.6733063
# nodegr 30.3986439 3.4347952
# re74 0.2159921 6.2271032
# re75 8.3863254 4.7320098
# u74 9.4140477 6.5848971
# u75 17.6809436 8.5502059
They may easily be plotted using matplot.
matplot(sad, pch=20, xaxt='n', main='Matching success',
ylab='Std. abs. diff.')
arrows(seq_along(comp[-2]), sad[, 1], seq_along(comp[-2]), sad[, 2],
length=.1, col=8)
axis(1, seq_along(comp[-2]), labels=comp[-2])
legend('topright', pch=20, col=1:2, leg=c('before matching', 'after matching'))
Note: R >= 4.1 used.
CodePudding user response:
Use the cobalt package, which was specifically designed for this purpose. If you decide to use a package other than Matching to perform the matching, for example, MatchIt or optmatch, cobalt works with them, too. See the cobalt website for information.
Importantly, cobalt requires minimal coding from the user and is extremely flexible producing whichever balance statistics you want and plots to display balance for covariates individually or overall. See below for some examples. I'll use the same example as jay.sf.
library(Matching)
#> Loading required package: MASS
#> ##
#> ## Matching (Version 4.9-11, Build Date: 2021-10-18)
#> ## See http://sekhon.berkeley.edu/matching for additional documentation.
#> ## Please cite software as:
#> ## Jasjeet S. Sekhon. 2011. ``Multivariate and Propensity Score Matching
#> ## Software with Automated Balance Optimization: The Matching package for R.''
#> ## Journal of Statistical Software, 42(7): 1-52.
#> ##
library(cobalt)
#> cobalt (Version 4.3.2.9000, Build Date: 2022-02-28)
data(lalonde, package = "Matching")
## Estimate propensity score
fit <- glm(treat ~ age I(age^2) educ I(educ^2) black
hisp married nodegr re74 I(re74^2) re75 I(re75^2)
u74 u75, family=binomial, data=lalonde)
lalonde$ps <- fit$fitted.values ## store ps in data set
## matching
rr <- with(lalonde, Match(Y=re78, Tr=treat, X=ps, M=5, caliper=.25))
Below we use bal.tab() to display balance statistics, including the treated group and control group means and the standardized mean differences before and after matching.
bal.tab(rr, formula = treat ~ age educ black hisp married nodegr re74 re75,
data = lalonde, un = TRUE, disp.means = TRUE)
#> Balance Measures
#> Type M.0.Un M.1.Un Diff.Un M.0.Adj M.1.Adj Diff.Adj
#> age Contin. 25.0538 25.8162 0.1066 25.0932 25.6023 0.0712
#> educ Contin. 10.0885 10.3459 0.1281 10.4271 10.3295 -0.0485
#> black Binary 0.8269 0.8432 0.0163 0.8523 0.8523 -0.0001
#> hisp Binary 0.1077 0.0595 -0.0482 0.0615 0.0625 0.0010
#> married Binary 0.1538 0.1892 0.0353 0.1770 0.1875 0.0105
#> nodegr Binary 0.8346 0.7081 -0.1265 0.7119 0.7273 0.0153
#> re74 Contin. 2107.0268 2095.5740 -0.0023 1755.7096 2062.6252 0.0628
#> re75 Contin. 1266.9092 1532.0556 0.0824 1377.3531 1530.7851 0.0477
#>
#> Sample sizes
#> Control Treated
#> All 260. 185
#> Matched (ESS) 160.99 176
#> Matched (Unweighted) 242. 176
#> Unmatched 18. 0
#> Discarded 0. 9
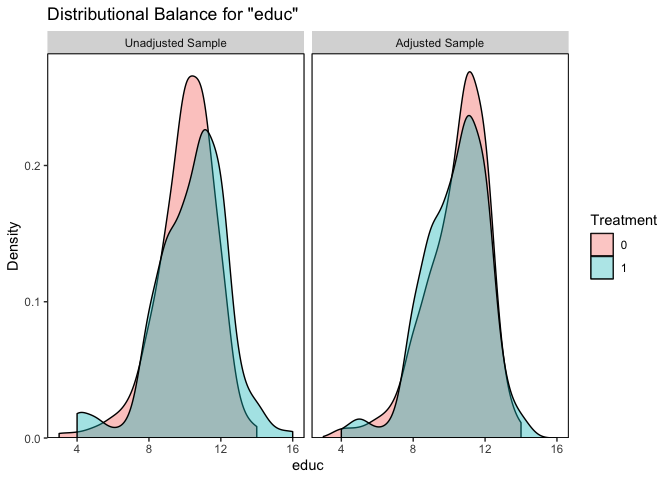
Below we use bal.plot() to examine distributional balance for a single covariate.
bal.plot(rr, formula = treat ~ age educ black hisp married nodegr re74 re75,
data = lalonde, var.name = "educ", which = "both")
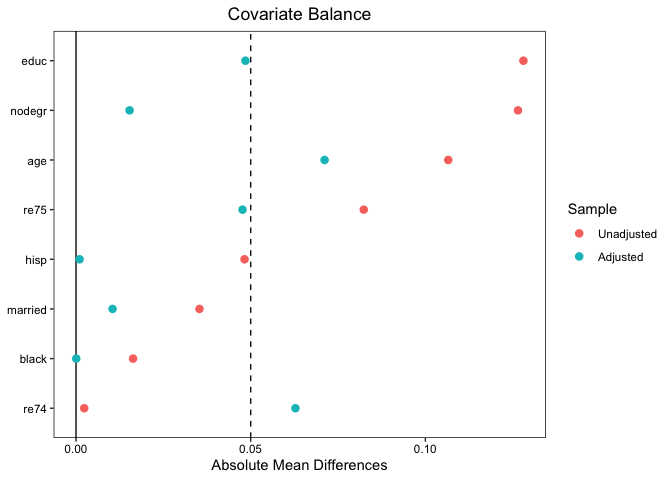
Below we create a Love plot using love.plot() to summarize balance in the sample. The plot is highly customizable; here I add a threshold line for standardized mean differences of .05.
love.plot(rr, formula = treat ~ age educ black hisp married nodegr re74 re75,
data = lalonde, abs = TRUE, var.order = "unadjusted", thresholds = c(m = .05))
Created on 2022-03-20 by the reprex package (v2.0.1)
There are many examples on the cobalt website and many ways to customize the tables and plots. It is meant to be easy to use for non-programmers.