Huffman Code Tree with Depth 1 less than number of letters-CodePudding

I need to create a Huffman Code tree using n letters and make the tree of depth n-1.

I tried making all the frequencies equal but it did not work for some values of n.

Is there any specific way to solve this

CodePudding user response：

To make the tree depth n-1 you need to set the probabilities as follows: for the iith letter, the probability should be 2^ii, where ii = 1,2,3,4,.... The probability of the last letter should just complete to a sum of 1.

Example

for the alphabet 0,1,2,3, giving the following probabilities:

p_0 = 0.5
p_1 = 0.25
p_2 = 0.125
p_3 = 1 - 0.5 -0.25 -0.125 = 0.125

The three will look as follows:

O
|----------|
0(0)       O
           |----------|
           1(10)      O
                      |----------|
                      2(110)     3(111)

Adding another letter to the alphabet will change the probabilities to:

p_0 = 0.5
p_1 = 0.25
p_2 = 0.125
p_3 = 0.0625
p_4 = 0.0625

And the new tree will look like:

O
|----------|
0(0)       O
           |----------|
           1(10)      O
                      |----------|
                      2(110)     O
                                 |----------|
                                 3(1110)    4(1111)

CodePudding user response：

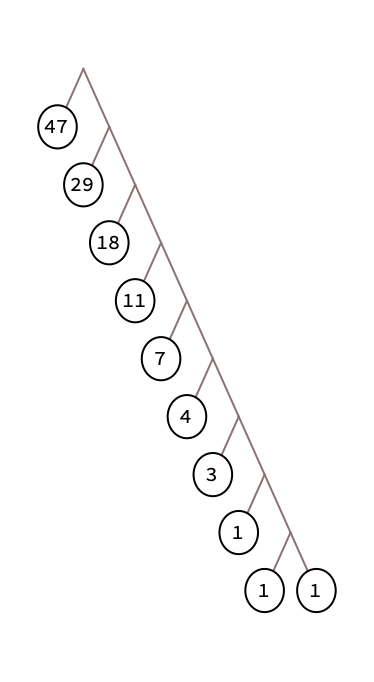
The set of frequencies to do this with the minimum sum is a modification of the Lucas numbers.

The Lucas number sequence starts with 2, 1, and continues with each number being the sum of the previous two numbers (just like the Fibonacci sequence, which instead starts with 1, 1).

2 1 3 4 7 11 18 29 47 ...

To get the longest Huffman code, replace that initial 2 with 1, 1:

1 1 1 3 4 7 11 18 29 47 ...

That sequence of n frequencies will result in the maximal-length Huffman code of n-1 bits.

The depth-nine tree is: