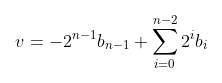How can I represent any negative value mathematically using summation?-CodePudding

For example, I know that I can represent the value -1 in this way, where "n" is the bit size of the type, n-1 is the most significant bit, and the value -2, which gives the complement representation of 2, plus the sum of the sum described below, now, I would like to know how I can use the sum, or any other type of calculation, to represent any negative value, in the form of a mathematical demonstration.

Assuming n has 8 bits, 8 - 1, 7, that is -2^7 = -128 127 = -1, I'm saying the summation will go through all the bits, such as 2^0 2^1, ..., 2^6, ie I ignore the most significant bit.

CodePudding user response：

Iiuc, the formula you gave does exactly what you're asking to do. You have answered your own question.

Let's do examples with n=4. For a reference, we can count in the negative direction to get all possibilities:

-1 = 1111
-2 = 1110
-3 = 1101
-4 = 1100
-5 = 1011
-6 = 1010
-7 = 1001
-8 - 1000

So now let's see if the formula gives correct results. By convention, a 4-digit binary number representation is four bits numbered 3 down to 0: b_3 b_2 b_1 b_0.

Example: 1111

This implies b_0 = b_1 = b_2 = b_3 = 1.

Substituting, you have v = -2^3x1 1x1 2x1 4x1 = -8 7 = -1.

Example: 1010

This implies b_0 = 0, b_1 = 1, b_2 = 0, b_3 = 1.

Substituting, you have v = -2^3x1 1x0 2x1 4x0 = -8 2 = -6.

You can work all the other values. They'll be correct.

The formula works for positive numbers, too. In that case b_3 = 0, so the -8 term goes away.