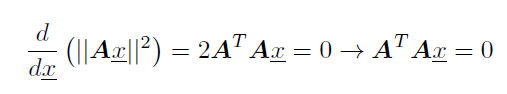This must be surely well known, being a particular linear programming problem. What I want is a specific easy to implement efficient algorithm adapted to this very case, for relatively small sizes (about, say, ten vectors of dimension less than twenty).

I have vectors v(1), ..., v(m) of the same dimension. Want an algorithm that produces strictly positive numbers c(1), ..., c(m) such that c(1)v(1) ... c(m)v(m) is the zero vector, or tells for sure that no such numbers exist.

What I found (in some clever code by a colleague) gives an approximate algorithm like this:

start with, say, c(1) = ... = c(m) = 1/m;

at each stage, given current approximation v = c(1)v(1) ... c(m)v(m), seek for j such that v - v(j) is longer than v(j).

If no such j exists then output "no solution" (or c(1), ..., c(m) if v is zero).

If such j exists, change v to the new approximation (1 - c)v cv(j) with some small positive c.

This changes c(j) to (1 - c)c(j) c and each other c(i) to (1 - c)c(i), so that the new coefficients will remain positive and strictly less than 1 (in fact they will sum to 1 all the time, i. e. we will remain in the convex hull of the v(i)).

Moreover the new v will have strictly smaller length, so eventually the algorithm will either discover that there is no solution or will produce arbitrarily small v.

Clearly this is incomplete and not satisfactory from several points of view. Can one do better?

CodePudding user response：

This is doable as follows.

First write your vectors as columns. Put them into a matrix. Now create a single column with entries c(1), c(2), ..., c(m_)). If you multiply that matrix times that column, you get your linear combination.

Now consider the elementary row operations. Multiply a row by a constant, swap two rows, add a multiple of one row to another. If you do an elementary row operation to the matrix, your linear combination after the row operation will be 0 if and only if it was before the row operation. Therefore doing elementary row operations DOESN'T CHANGE the coefficients that you're looking for.

Therefore you may simplify life by doing elementary row operations to put the matrix into The column of V matching with the lowest eigenvalue in the diagonal matrix Sigma will be your solution.

Explanation

When we want to minimize the Ax = 0 in the MSE sense, we can compute the vector derivative w.r.t x as follows:

Therefore, the eigenvector of A^TA matching the smallest eigenvalue will solve your problem.

Practical solution example

In python, you can use numpy.linalg.svd to perform the SVD decomposition. numpy orders the matrices U and V^T such that the leftmost column matches the largest eigenvalue and the rightmost column matches the lowest eigenvalue. Thus, you need to compute the SVD and take the rightmost column of the resulting V:

from numpy.linalg import svd
[_, _, vt] = svd(A)
x = vt[-1]  # we take the last row since this is a transposed matrix, so the last column of V is the last row of V^T

• The equations are taken from one of my summaries and therefore I do not have a link to the source