Manhattan Matrix by 2 Matrices is non symmetric but should be-CodePudding

I created two matrices that have random integers as components, the dimension of the matrix doesn't matter. Then I want to calculate the distance matrix by the Manhattan method and frame it as a matrix. The matrix should be symmetric, but when I frame it as a matrix, the output is a non symmetric distance matrix.

By that matrix (that should be the output) I want to calculate a cluster.

Where is my mistake?

Code:

a <- c(sample.int(30,6))

b <- c(sample.int(30,6))

c <- c(sample.int(30,6))

d <- c(sample.int(30,6))

e <- c(sample.int(30,6))

f <- c(sample.int(30,6))

V2 <- rbind(a,b,c,d,e,f)

V1 <- rbind(a,b,c,d,e,f) 

d1MNR <- matrix(dist(Vorlage1,Vorlage2, method="manhattan"))              #### Is non symmetric
          
d1MR  <- matrix(dist(V1,V2,upper=TRUE, diag=TRUE ,method="manhattan"))    #### Should be symmetric, but is not     

d1MR ### Generate output


hclust <- hclust(dist(d1MR), method = "single")                         ### Clustering

CodePudding user response：

You can make a symmetrical distance matrix from V1 or a symmetrical matrix from V2, but the only way to make a symmetric matrix from both of them together is to combine them V12 <- rbind(V1, V2). The dist() function returns a dist object that hclus can use. You do not need to convert them to a matrix. In your example V1 and V2 are identical. We need them to be different:

set.seed(42)
V1 <- matrix(sample.int(30, 36, replace=TRUE), 6)
V2 <- matrix(sample.int(30, 36, replace=TRUE), 6)
V12 <- rbind(V1, V2)
rownames(V12) <- paste(rep(c("V1", "V2"), each=6), 1:6, sep=":")
colnames(V12) <- letters[1:6]
V12
#       a  b  c  d  e  f
# V1:1 17 18  4 18  4 28
# V1:2  5 26 25 15  5  8
# V1:3  1 17  5  3 13  3
# V1:4 25 15 14  9  5 26
# V1:5 10 24 20 25 20  1
# V1:6  4  7 26 27  2 10
# V2:1 24  8 28  3 18 22
# V2:2 30  4  5 24  6 21
# V2:3 11  4  4 23  6  2
# V2:4 15 22  2 17  2 23
# V2:5 22 18 24 21 20  6
# V2:6 26 13 18 26  3 26
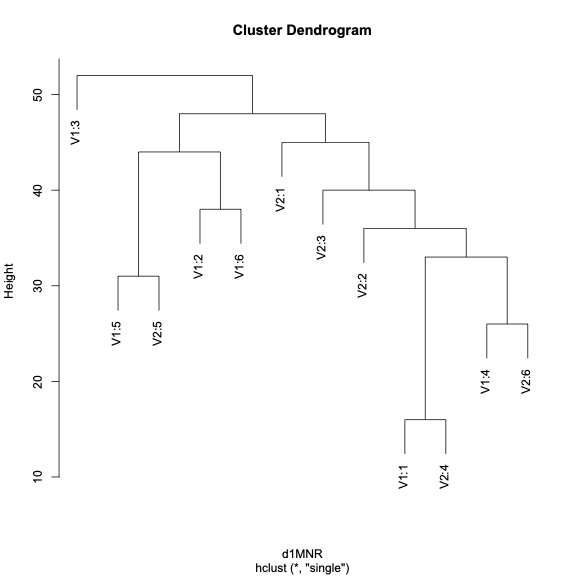
d1MNR <- dist(V12, method="manhattan")
hclust <- hclust(d1MNR, method = "single")
plot(hclust)

If you want to look at a symmetrical distance matrix:

print(d1MNR, upper=TRUE, diag=TRUE)
#      V1:1 V1:2 V1:3 V1:4 V1:5 V1:6 V2:1 V2:2 V2:3 V2:4 V2:5 V2:6
# V1:1    0   65   67   33   79   75   76   43   53   16   66   39
# V1:2   65    0   58   66   44   38   79   90   64   57   49   72
# V1:3   67   58    0   72   62   76   79   88   52   67   69   98
# V1:4   33   66   72    0   86   78   45   46   74   43   63   26
# V1:5   79   44   62   86    0   58   83   90   54   73   31   72
# V1:6   75   38   76   78   58    0   75   68   48   73   59   54
# V2:1   76   79   79   45   83   75    0   67   93   80   52   59
# V2:2   43   90   88   46   90   68   67    0   40   49   73   36
# V2:3   53   64   52   74   54   48   93   40    0   55   65   68
# V2:4   16   57   67   43   73   73   80   49   55    0   72   49
# V2:5   66   49   69   63   31   59   52   73   65   72    0   57
# V2:6   39   72   98   26   72   54   59   36   68   49   57    0