Calculate the normal vector of a line defined by two points toward another point-CodePudding

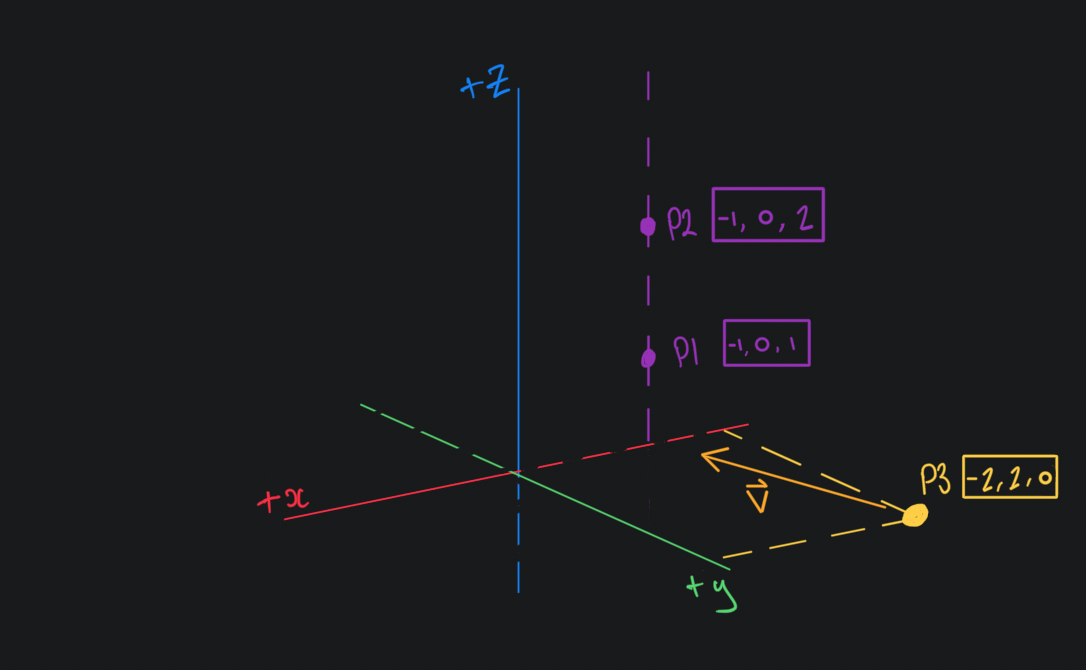
This can probably be classed as more of a math question than a Three.js question however I've come across the issue whilst using Three.

Say I have two instances of Vector3 that can define a line (P1 and P2 in image below).

Now say I also have another instance of a Vector3 to represent a point (P3). I want to calculate the vector that defines the direction from P3 toward the line. The resulting vector should also be normal to the line.

I figure it is a dot/cross product problem but can't quite get it.

The equation should work even when P1 and P2 define a line which is not parallel to any of the cartesian axes.

CodePudding user response：

Yes, it is a question of dot product:

compute Vector3 vn:

vn = ( p2 - p1 ).normalize();

and vp:

vp = ( p3 - p1 );

Then use dot product to calculate projection of vp over p2-p1 line:

v = vp.dot( vn ) * vn;

then

p1   v

is the intersection point you are looking for

CodePudding user response：

For Three.js users, after following the steps provided by Jordi, here is some code that lets you lerp a point toward the line.

Instead of calculating v like this: v = vp.dot( vn ) * vn - Vector3 has a method projectOnVector to make this a bit smoother.

interface IProjectTowardAxis {
  points: Vector3[];
  /** The first point to define a line */
  p1: Vector3;
  /** The second point to define a line */
  p2: Vector3;
  /** lerp distance from 0 to 1 */
  alpha: number;
}

const projectPointsTowardAxis = (options: IProjectTowardAxis): Vector3[] => {
  const {points, p1, p2, alpha} = options;

  const vn = p2.clone().sub(p1).normalize();

  for (let pt of points) {
    const vp = pt.clone().sub(p1);
    const v = vp.clone().projectOnVector(vn);
    vp.copy(p1).add(v);
    pt.lerp(vp, alpha);
  }
  return points;
};

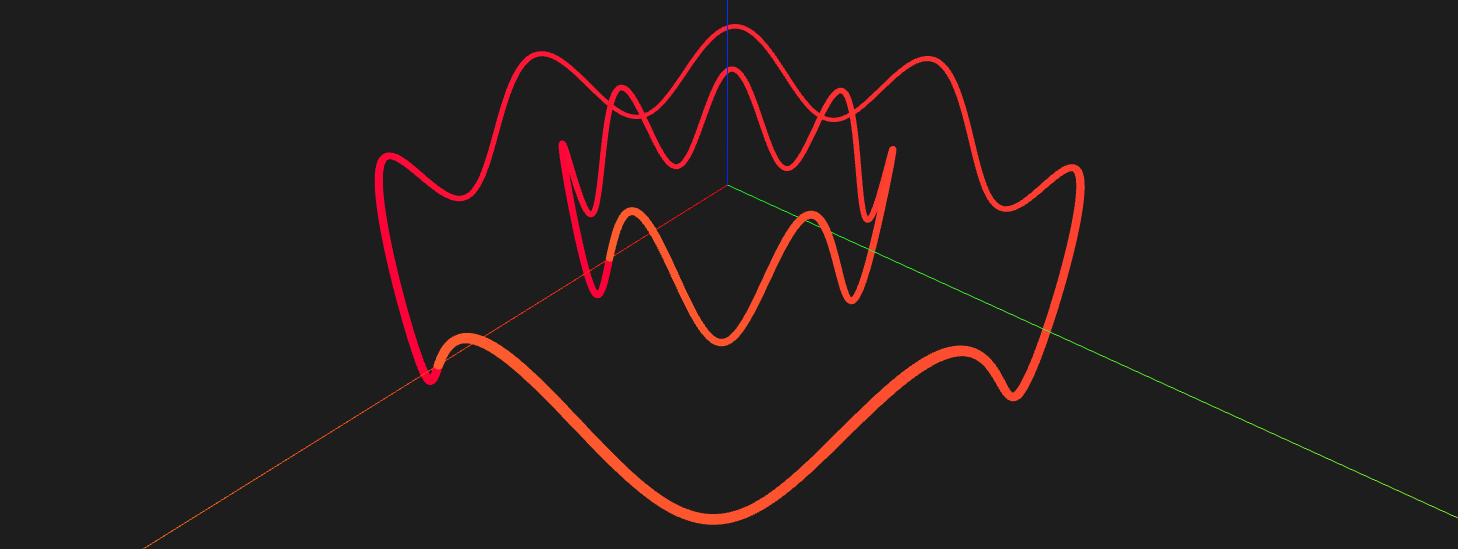
Using this function, the outer wave was projected toward the z-axis.