Graphing Piecewise Differential Equation in Matplotlib-CodePudding

I am trying to graph a piecewise differential equation

dA/dt = r-c*A

Where D(t)=r for r<h, where r is some fixed rate in mg/hour, and h is some time in hours. At t=h, the dosing stops, so D(t)=0.Dosing rate for constant intravenous dosing for h=4 hours. I would like to graph the piecewise function for 0<t<h and for t is greater than h (r=0)

Here is the code I have so far: .

#Function that returns dA/dt
# 0<t<h
def model(A,t):
    c=0.35
    r=10
    dAdt = r-c*A
    return dAdt

#initial condition 
A0=10

#time points 
t=np.linspace(0,20)

#solve ODE

A= odeint(model,A0,t)

plt.plot(t,A)
plt.xlabel('time')
plt.ylabel('A(t)')
plt.show()

CodePudding user response：

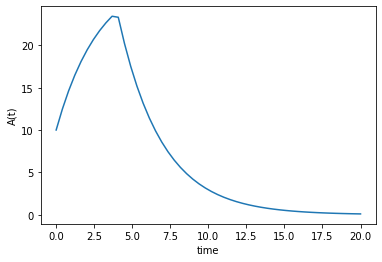
I'm not really sure if I fully understand your question. Does the following help?

from scipy.integrate import odeint
h = 4

#Function that returns dA/dt
# 0<t<h
def model(A,t):
    c=0.35
    r=10 if t < h else 0
    dAdt = r-c*A
    return dAdt

#initial condition 
A0=10

#time points 
t=np.linspace(0,20)

#solve ODE

A= odeint(model,A0,t)

plt.plot(t,A)
plt.xlabel('time')
plt.ylabel('A(t)')
plt.show()

CodePudding user response：

It might help to understand the code later if you write it close to the mathematical formulas you use

def D(t): return r if t<h else 0

def model(A,t,c): dAdt = D(t)-c*A; return dAdt

A= odeint(model,A0,t,args=(c,))