Optimized algorithm to check if a line segment is covered by a list of polygons-CodePudding

This problem was solved using the sympy library, however, I believe my solution is not optimal and I am looking for a better algorithm. Answers that utilize better data structures than the ones I have used are welcomed however, other libraries used as a substitute for sympy(Ex: shapely) will not be considered the correct answer.

I am trying to solve a problem involving a line segment and a bunch of polygons. I have used a list to hold all my polygons. A polygon is then plotted on a 2D space and a check is conducted to see if the entire or part of the line segment is obscured by the current polygon. If yes, then the line segment part getting obscured by the polygon is chopped and only the visible part wrt to the current polygon remains.

In the next step, another polygon from the list is plotted but this time the check is conducted on the visible part of the line segment produced from the previous step. In this way, all the parts of the line segment that are obscured by the polygons are dropped and finally, I am left with a list that is either empty or not. If the list is empty, it means that all the polygons cover the line segment and True is returned. If not, it means there is a portion of the line that is visible and not covered by all the polygons so a False is returned.

I hope the screenshots below make the problem statement clearer.

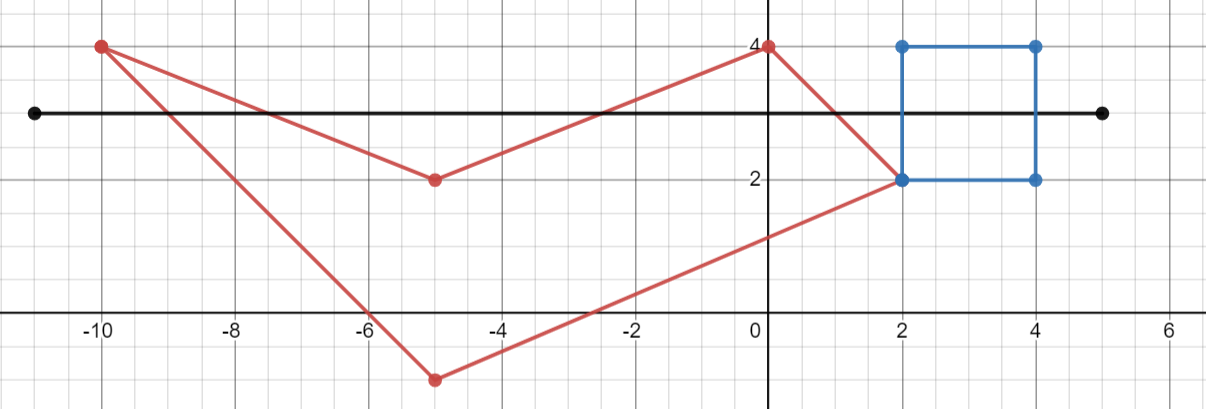
In the case above, you can see all the polygons don't fully cover the line segment, hence, the code for this problem will return True.

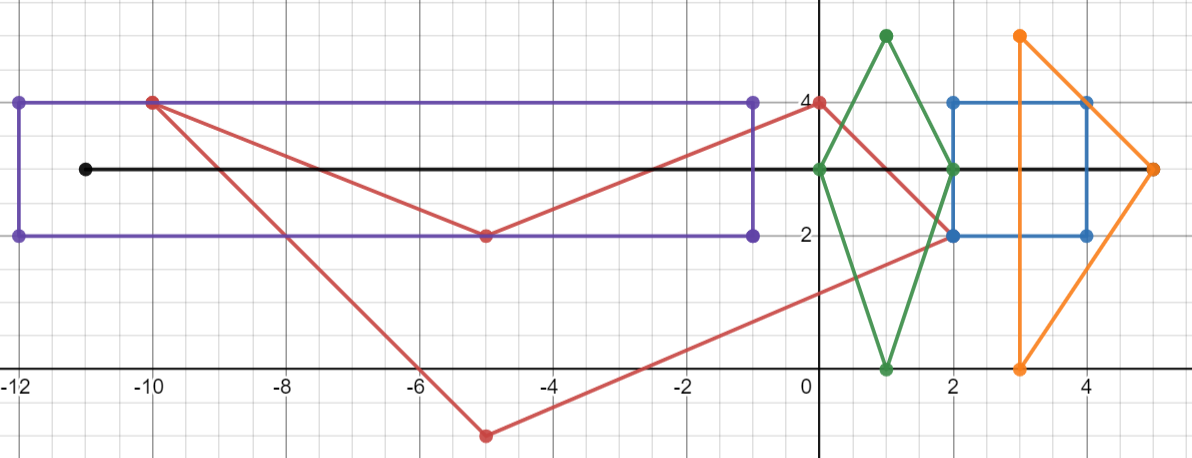
In this image, all the polygons completely cover the line segment, hence the code will return False here.

EDIT:

@MattTimmermans brought up a great point which alerted me to a couple of possible edge cases where a line segment can lie on the boundary of the polygon. In such cases the encloses() sympy method will return False when the actual desired behaviour for it is to return True. I have modified the code to account for that edge case. Furthermore, the blue polygon's boundary lies exactly on the line segment and calling the intersect method will result in a Segment2D object being returned and not the points. To account for this I have created a new function called sortAllPoints().

This screenshot below will illustrate this scenario better.

Here is my solution to the problem statement defined using a brute force technique.

from sympy import Polygon, Point, Segment2D 

def sortAllPoints(intersectionSet, pointsOnLine, currentLine, polygon):
    # Do nothing if it is an empty set
    if not isinstance(intersectionSet, sympy.sets.sets.EmptySet):
        # Check if the intersection is a sympy.Segment2D object.
        if isinstance(intersectionSet, Segment2D):
            pointsOnLine.extend([intersectionSet.p1, intersectionSet.p2])
        # Check if the intersection is a sympy.sets.set.Union object. 
        elif isinstance(intersectionSet, sympy.sets.sets.Union):
            deserializedPoints = []
            for entity in intersectionSet.args:
                if isinstance(entity, Segment2D):
                    deserializedPoints.append(entity.p1)
                    deserializedPoints.append(entity.p2)
                elif isinstance(entity, Point):
                    deserializedPoints.append(entity)
            pointsOnLine.extend(deserializedPoints)
        else:
            pointsOnLine.extend(iter(polygon.intersect(currentLine)))

    sortedPoints = sorted(pointsOnLine, key=lambda coordinates: (coordinates[0], coordinates[1]))
    return sortedPoints

def lineFragments(line, listPolygon):

    # line is of type sympy.Segment2D. 
    # listPolygon contains [sympy.Polygon]

    activeLine = line
    
    # Contains sympy.Segment2D objects. The length of this list determines whether this function should return True or False.
    visibleFragments = []
    
    # iterate through the list of sympy.Polygon objects.
    for index, polygon in enumerate(listPolygon):
        
        # This is a list of lists. This was done so particularly because I don't want to create a line segment between points that have already been processed. This helps me isolate and work with only the line segments that are visible from the previous iteration.
        allSortedPoints = []

        if index == 0:
            pointsOnLine = [activeLine.p1, activeLine.p2]
            # Get all the points where the polygon intersects with the line segment.
            pointsOnLine.extend(iter(polygon.intersect(activeLine)))
            sortedPoints = sortAllPoints(intersectionSet, pointsOnLine, activeLine, polygon)
            allSortedPoints.append(sortedPoints)
        
        # Break out of the loop if the line segment has been completely covered by the polygons before it. 
        elif not visibleFragments:
            return False

        else:
            # Find the intersection points between the polygon and all the visible parts of the line segment that were computed in the previous iteration.
            for lineFragment in visibleFragments:
                pointsOnLine = [lineFragment.p1, lineFragment.p2]
                pointsOnLine.extend(iter(polygon.intersect(lineFragment)))
                sortedPoints = sortAllPoints(intersectionSet, pointsOnLine, activeLine, polygon)
            allSortedPoints.append(sortedPoints)

        tempList = []

        for sortedPoints in allSortedPoints:
            for idx, currentPoint in enumerate(sortedPoints):
                if idx < len(sortedPoints) - 1:

                    # Create a line segment using the points.
                    segment = Segment2D(currentPoint.evalf(3), sortedPoints[idx   1].evalf(3))
                    # Use the sympy.Polygon.encloses method to determine if the polygon covers the current fragment of the line segment.
                    if isinstance(segment, Segment2D) and not polygon.encloses(segment.midpoint) and not \
                            polygon.contains(segment.midpoint):
                        tempList.append(segment)
        
        # Update the list of visible line segments, so that there is no data carry over from iterations previous to this.
        visibleFragments = tempList

    if not visibleFragments:
        return False

    return True


def main():
    # Experiment 1.
    polygon1 = Polygon(Point(-10, 4), Point(-5, -1), Point(2, 2), Point(0, 4), Point(-5, 2))
    polygon2 = Polygon(Point(2, 2), Point(4, 2), Point(4, 3), Point(2, 3))
    # polygon2 = Polygon(Point(2, 2), Point(4, 2), Point(4, 4), Point(2, 4))
    line2 = Segment2D(Point(-11, 3), Point(5, 3))
    listPolygons1 = [polygon1, polygon2]
    booleanVal1 = lineFragments(line2, listPolygons1)
    print(booleanVal1)

    # Experiment 2.
    polygon3 = Polygon(Point(-1, 2), Point(-12, 2), Point(-12, 4), Point(-1, 4))
    polygon4 = Polygon(Point(3, 5), Point(3, 0), Point(5, 3))
    listPolygons2 = [polygon1, polygon2, polygon3, polygon4]
    # booleanVal2 = lineFragments(line2, listPolygons2)
    # print(booleanVal2)

    # Experiment 3.
    polygon5 = Polygon(Point(1, 5), Point(0, 3), Point(1, 0), Point(2, 3))
    polygon6 = Polygon(Point(2, 2), Point(9, 2), Point(9, 3), Point(4, 3), Point(4, 5), Point(3, 5), Point(3, 3),
                       Point(2, 3))
    listPolygons3 = [polygon1, polygon6, polygon2, polygon3, polygon4, polygon5]
    # print(polygon6.area)
    # line3 = Segment2D(Point(0, 6), Point(0, -6))
    # print(type(polygon2.intersect(line2)))
    # booleanVal3 = lineFragments(line2, listPolygons3)
    # print(booleanVal3)

Im looking for a solution with code as well as links to reading material that I can use to better myself. If you have got this far, thank you for your time.

CodePudding user response：

Let P be your list of polygons, a and b be the end points of your curve/segments. Let A be the list of polygons that contains a, similar definition for B. You should be able to build these efficiently enough. If A or B is empty, return True.

suppose there exist p in A intersection B. Count the intersection of [a,b] with p. If theres is none, the answer is False, as P entirely contains the curve. If there is for instance two intersection (notice it must always be an even number), say a' and b', call the function on curve (a', b') and P-p. If there are 2k intersection, do multiple similar calls.

Suppose a and b are inside different polygons. Let a' be farthest vertex that is on the curve such that there exist some polygon p_a in A, such that [a,a'] is in p_a. Define b' in similar way. Call the function on (a', b') and P.

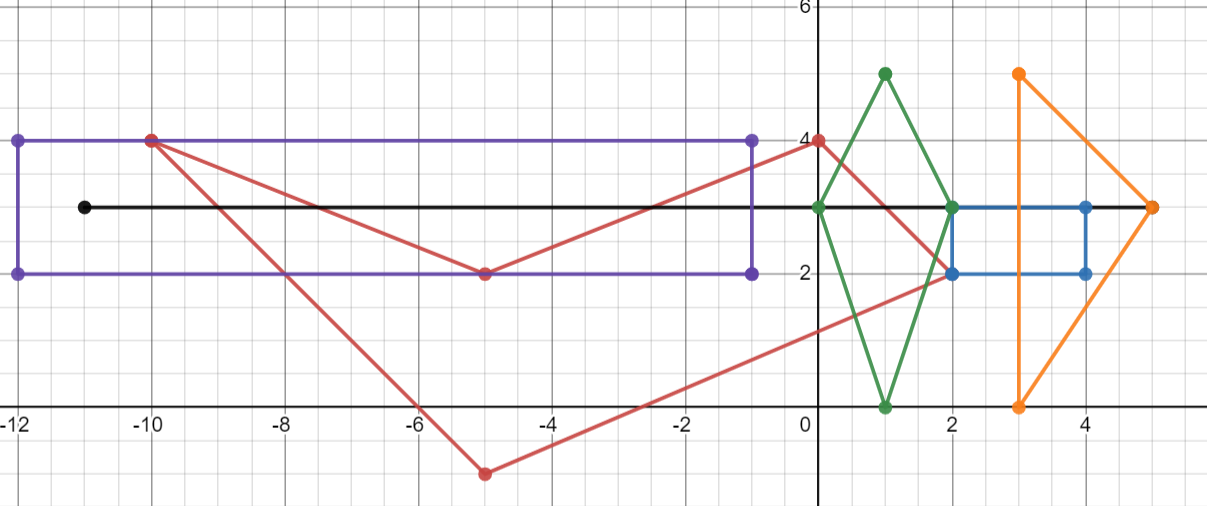
Example of execution (based on your second example):
Let denote the point by their position on horizontal axis.
First call: a = -11, b =5. a and b are both contained in some polygon, but different. A = purple, B = yellow. a' = -1, b'=3.
Second call: a = -1, b=3. They are both contained in some polygon, but different. A = purple, red; B = yellow, blue. a' = 1, b=2.
Third call: a=1, b=2. Both are contained in green. Green polygon does not intersect (a,b), so we may return false.

CodePudding user response：

Imagine walking along the line that contains the target line segment.

Keep a counter. Increment it each time you enter a polygon, and decrement it every time you leave a polygon.

If your counter is at 0 for any non-zero distance inside the line segment, then the line segment is not entirely obscured.

To turn this into an efficient algorithm for your problem:

For each polygon, generate the lists of entry and exit positions by intersecting with the line (be careful of the boundary conditions)
Merge all the entry position lists and sort
Merge all the exit position lists and sort
walk through the lists to check the above condition.

The total time would be O(N log N) in the number of polygon edges.