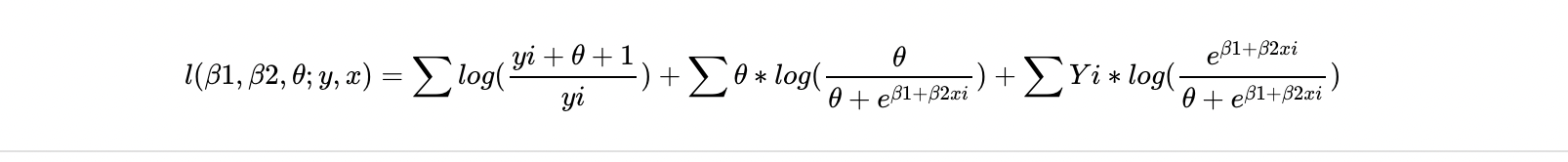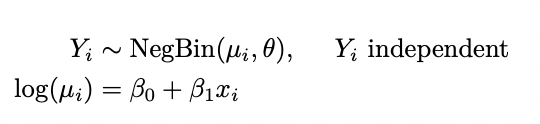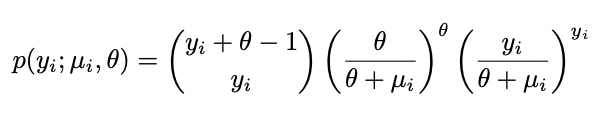I have the following log-likelihood from my model which i am trying to write as a function in R.
My issue come as i dont know how to write theta in terms of the the function. I have had a couple of attempts at this as shown below, any tips/advice on if these are close to being correct could be appreciated.
function with theta written as theta
#my likelihood function
mylikelihood = function(beta) {
#log-likelihood
result = sum(log(dengue$cases theta 1 / dengue$cases))
sum(theta*log(theta / theta exp(beta[1] beta[2]*dengue$time)))
sum(theta * log(exp(beta[1] beta[2]*dengue$time / dengue$cases exp(beta[1] beta[2]*dengue$time))))
#return negative log-likelihood
return(-result)
}
my next attempt with thetas replaced with Xi from my dataset, which here is (dengue$time)
#my likelihood function attempt 2
mylikelihood = function(beta) {
#log-likelihood
result = sum((log(dengue$Cases dengue$Time 1 / dengue$Cases)))
sum(dengue$Time*log(dengue$time / dengue$Time exp(beta[1] beta[2]*dengue$Time)))
sum(dengue$Cases * log(exp(beta[1] beta[2]*dengue$Time / dengue$Cases
exp(beta[1] beta[2]*dengue$Time))))
#return negative log-likelihood
return(-result)
}
data
head(dengue)
Cases Week Time
1 148 36 1
2 275 37 2
3 205 38 3
4 133 39 4
5 123 40 5
6 138 41 6
Are either of these close to being correct, and if not where am I going wrong?
Updated into about where the log-likelihood comes from;
The model;
Negative Binomial distribution with mean µ and dispersion parameter θ has pmf;
CodePudding user response:
The fundamental problem is that you have to pass both beta (intercept and slope of one component of the problem) and theta as part of a single parameter vector. You had other problems with parenthesis placement that I fixed, and I reorganized the expressions a little bit.
There are several more important mistakes in your code.
- The first term is not a fraction; it is a binomial coefficient. (i.e., you should use
lchoose(), as shown below) - You changed a 1 to a -1 in the first term.
nll <- function(pars) {
beta <- pars[1:2]
theta <- pars[3]
##log-likelihood
yi <- dengue$Cases
xi <- dengue$Time
ri <- exp(beta[1] beta[2]*xi)
result <- sum(lchoose(yi theta - 1,yi))
sum(theta*log(theta / (theta ri)))
sum(yi * log(ri/(theta ri)))
##return negative log-likelihood
return(-result)
}
read data
dengue <- read.table(row.names = 1, header = TRUE, text = "
Cases Week Time
1 148 36 1
2 275 37 2
3 205 38 3
4 133 39 4
5 123 40 5
6 138 41 6
")
fitting
Guessing starting parameters of (1,1,1) is a bit dangerous - it would make more sense to know something about the meaning of the parameters and guess biologically plausible values - but it seems to be OK.
nll(c(1,1,1))
optim(par = c(1,1,1), nll)
Since we didn't constrain theta to be positive we get some warnings about taking the log of a negative number, but these are probably harmless (e.g. see here)
alternatives
R has a lot of built-in machinery for fitting negative binomial models (I should have recognized what you were doing!)
MASS::glm.nb sets everything up for you automatically, you just have to specify the predictor variables (it uses a logarithmic link and adds an intercept, so specifying ~Time will make the mean equal to exp(beta0 beta1*Time)).
library(MASS)
glm.nb(Cases ~ Time, data = dengue)
bbmle is a little bit less automated, but more flexible (here I am fitting theta on the log scale to avoid trying any negative values)
library(bbmle)
mle2(Cases ~ dnbinom(mu = exp(logmu), size = exp(logtheta)),
parameters = list(logmu ~ Time),
data = dengue,
start = list(logmu = 0, logtheta = 0))
All three of these approaches (corrected negative log-likelihood function optim, MASS::glm.nb, bbmle::mle2) give the same results.