Will Dijkstra's shortest path algorithm return correct results on a directed tree with negative weight edges?
On a general graph with negative weights, the algorithm will fail, but since it’s a directed tree it feels like the algorithm will succeed.
CodePudding user response:
From other answers, you know that there is no good reason to run Dijkstra's algorithm if you know that the graph is a tree.
If you do run it, though, it will work even if the tree has negative edge weights.
The reason that Dijkstra's algorithm doesn't work for graphs with negative weights, is that negative weights allow a 2nd, shorter, path to be found to a vertex after its distance has already been decided. In a tree there are no 2nd paths.
CodePudding user response:
In a tree there is only one path between any two given nodes, so searching for the "shortest" path in a tree makes little sense: when you find a path it is the shortest, and this search does not need to take weights into account, so there is no need to use Dijkstra's algorithm. A simple depth-first search will do.
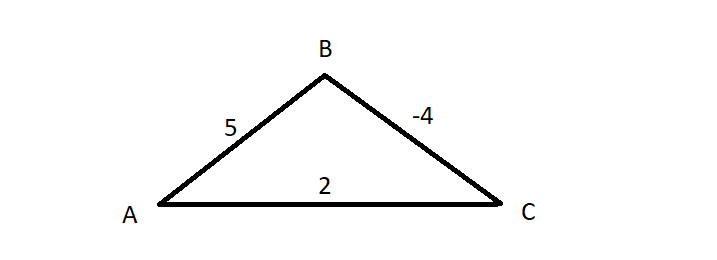
If the graph is not a tree, but a directed acyclic graph (DAG) with negative edges, then Dijkstra's algorithm cannot be used to find a shortest path. Take this counter example:
If we have to look for the shortest path from A to C, Dijkstra's algorithm will proceed to visit B and C, and as it hits the target, it will stop looking further, never considering the edge from B to C.
Other attempts to apply Dijkstra
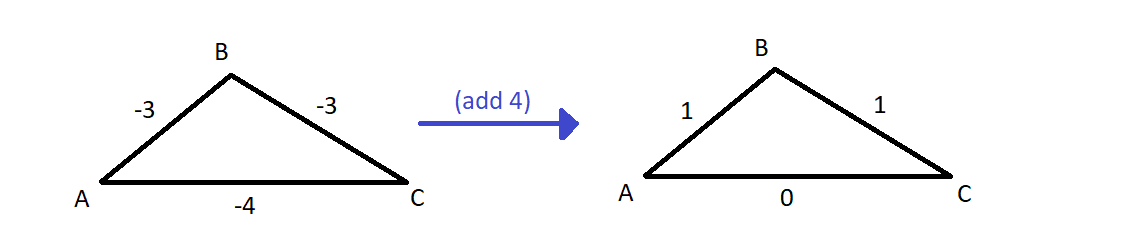
Another answer proposes to make all edge weights positive by adding an absolute value to all weights, but this does not yield correct results: what is the shortest path in the original graph, is not guaranteed to be still the shortest path in the derived graph.
Counter example:
Where in the original graph the shortest path from A to C runs via B, in the adjusted graph, the shortest path is A-C.
CodePudding user response:
If you have a tree, then depth first search will give you the only, cheapest path.
If you have a DAG, to find the shortest path use Dijkstra after doing a little preparatory work:
- Iterate over edges to find most negative weight
- Add absolute value of most negative weight to every edge weight.
- Apply Dijkstra