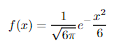How to numerically solve for the upper bound of a definite integral in Matlab?-CodePudding

Given the equation

For some given function f(x) where gamma is also given, how can you numerically solve for upper bound u in Matlab?

f(x) can be a placeholder for any model.

This is a root-finding and integration problem but with my lack of knowledge in Matlab, I'm still trying to figure out how it is done.

My initial solution is a brute force approach. Let's say we have

and gamma = 0.8, we can find the definite integral from -inf to u by extracting its integral from some very small value u, working our way up until we reach a result gamma = 0.8.

syms f(x)
f(x) = (1/(sqrt(6*pi)))*exp(-(x^2/6));  
gamma = 0.8;
u = -10;

res = int(f,x,-Inf,u);
while double(res) <= gamma
    u = u 0.1;
    res = int(f,x,-Inf,u);
end
fprintf("u is %f", u);

This solution is pretty slow and will definitely not work all the time.

I set u = 10 because looking at the graph of the function, we don't really get anything outside the interval [-5, 5].

CodePudding user response：

You can use MATLAB Symbolic Math Toolbox (an addon you might need to install). That way you can define yourself a "true" unknow variable x (not an array of x-values) and later integrate from negative infinity:

syms f(x)
f(x) = exp(2*x)  % an example function
gamma = int(f,x,-Inf,u)

This yields gamma as the integral from -Inf to u, after defining f(x) as a symbolic function and u as a scalar