Angle between 2 planes-CodePudding

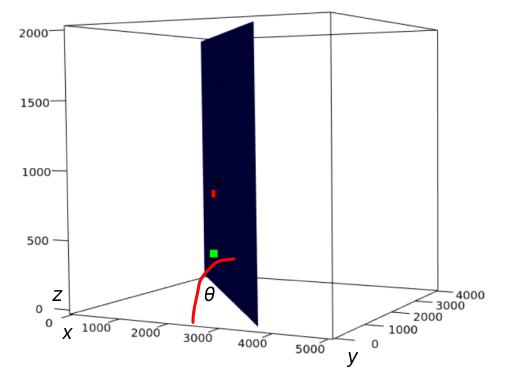
I have the equation of a plane. I would like to obtain the angle between this plane and the plane formed by the x and y axes.

Here is an illustration:

CodePudding user response：

If your equation of the plane is in form of

 ax   by   cz   d = 0

hence the equation of x-y plane is

z = 0

then by using this function it will return the angle in degree

ang_degree <- function(a , b , c){
    acos(abs(c)/sqrt(a^2   b^2   c^2))*180/pi
}

if you want it in radian remove *180/pi

CodePudding user response：

Given the equations of the two planes:

A1x   B1y   C1z   D1 = 0
A2x   B2y   C2z   D2 = 0

where A, B, C and D are the plane coefficients, then the angle between the two planes is given by the following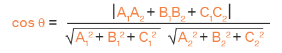

The equation of the second plane will be much simpler, i.e. z = 0.

CodePudding user response：

The angle between two planes is the same as the angle between the normals of these planes.

If ax by cz d = 0 is the plane equation then (a,b,c) is a normal of this plane.

Then use the dot product:

dot_product(normal1, normal2) = cos(the_angle) * norm(normal1) * norm(normal2)

Then acos to get the angle.