ValueError: Could not find root within given tolerance.How to solve?-CodePudding

i'm triyng to solve this equation using "nsolve" function. unfortunately, this error appears:

ValueError: Could not find root within given tolerance. (435239733.760000060718 > 2.16840434497100886801e-19)
Try another starting point or tweak arguments.

The code is:

import sympy

d=[0.3, 32.6, 33.4, 241.7, 396.2, 444.4, 480.8, 588.9, 1043.9, 1136.1, 1288.1, 1408.1, 1439.4, 1604.8]
N=len(d)
x = sympy.Symbol('x', real=True)
expr2 = sympy.Eq(d[13]   N * sympy.Pow(x, -1) - N * d[13] * sympy.Pow(1 - sympy.exp(-d[13] * N), -1), 0)
expr_2 = sympy.simplify(expr=expr2)
solution = sympy.nsolve(expr_2, -0.01)
s = round(solution, 6)
print(s)

CodePudding user response：

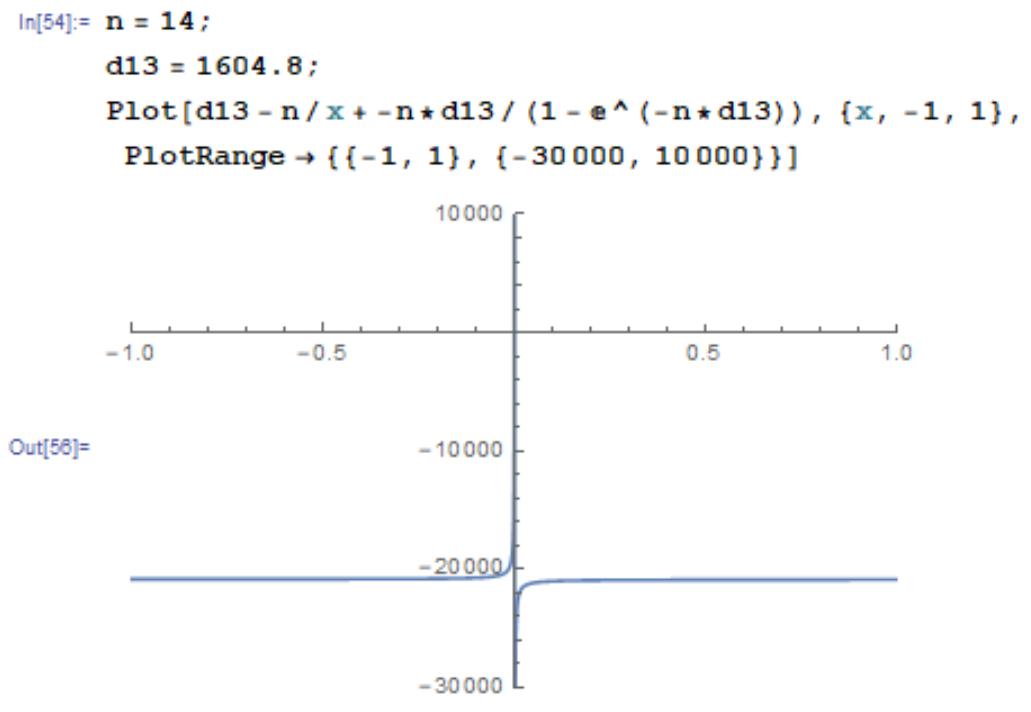
The system you are trying to solve leads to large derivatives and very abrupt changes, including a singularity at x == 0. This is the graph of the equation (Using Mathematica).

Numerical solvers struggle with these functions because most of them assumes some amount of smoothness around the solution and can be confused around singularities. Almost all of them (I'm talking about solvers in general, not just SymPy) benefits from regularization or a reformulation of the problem.

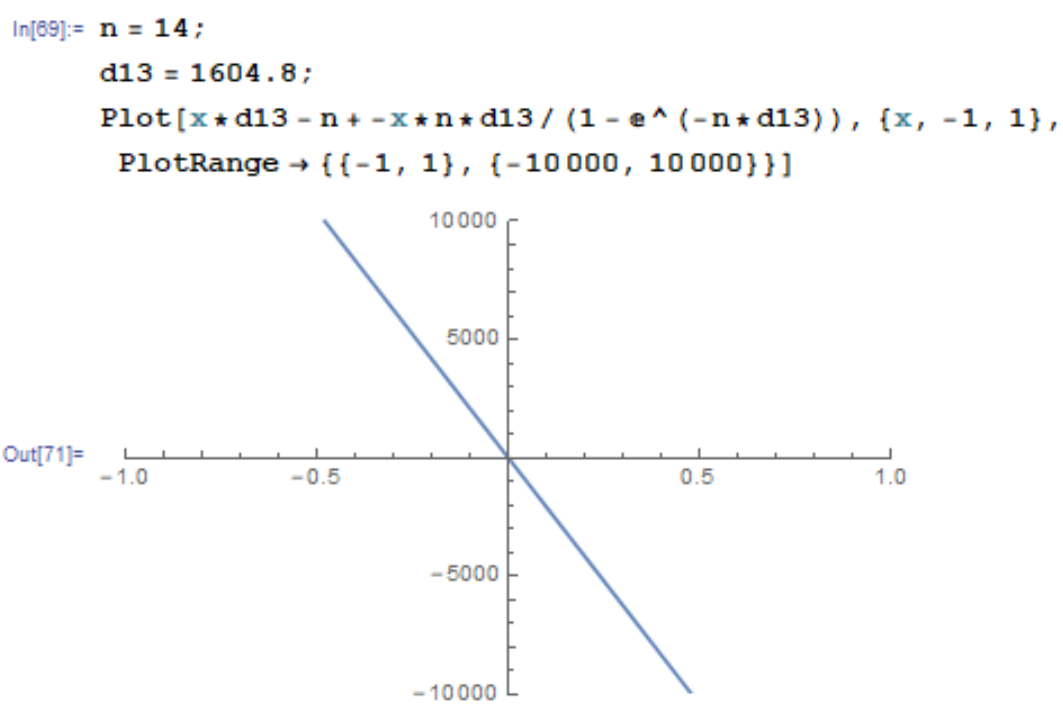
I would suggest to simplify the equation by multiplying both sides by x, which would remove the division by x and lead to a smoother function (linear in this case), for which numerical solvers behave correctly.

With this reformulation, you should find that the solution is 0.000671064.

Moreover, I would also suggest to rescale the coefficients so that they are all in [-1,1]. This also generally helps solvers. In your case, it will find the solution easily since it is linear, but more complex equations might cause problems.

CodePudding user response：

In this case who i can find a aproximated solution like you did in the other equation? I tried to simplify the equation by multiplying both sides by x like you did before, but don't work. Have any suggestion? thank you. the code is

import sympy

d=[0.3, 32.6, 33.4, 241.7, 396.2, 444.4, 480.8, 588.9, 1043.9, 1136.1, 1288.1, 1408.1, 1439.4, 1604.8]

N = len(d)

cl = list()

tot = sum(d)

print(tot)

x = sympy.Symbol('x', real=True)

expr2 = sympy.Eq(tot N * sympy.Pow(x, -1) - N * d[N-1] * sympy.Pow(1 - sympy.exp(-d[N-1]*x ), -1), 0)

expr_2 = sympy.simplify(expr=expr2)

solution = sympy.nsolve(expr_2, -0.01)

s = round(solution, 8)

print(s)