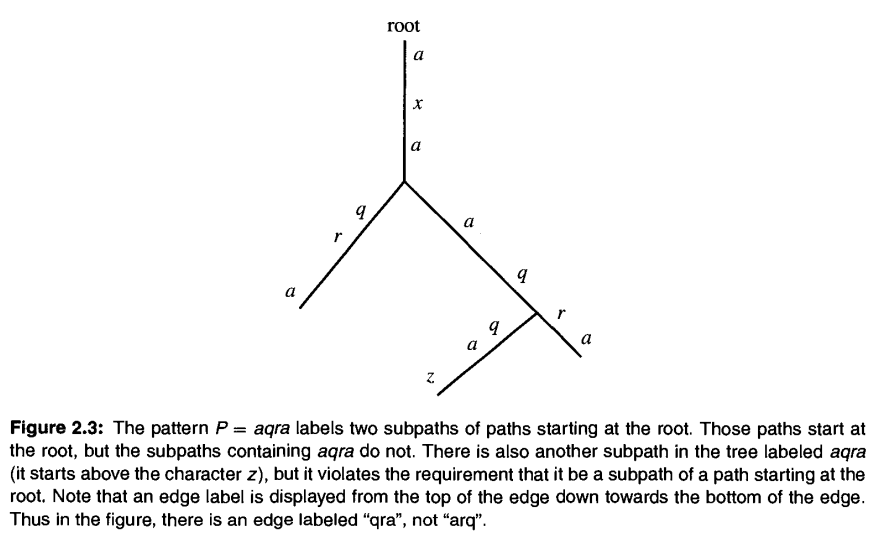
I am currently studying Dan Gusfield book (Algorithms on Strings, Trees and Sequences) and I am trying to solve the below exercise:

Suppose we are given a tree where each edge is labeled with one or more characters, and we are given a pattern P. The label of a subpath in the tree is the concatenation of the labels on the edges in the subpath. The problem is to find all subpaths of paths starting at the root that are labeled with pattern P. Note that although the subpath must be part of a path directed from the root, the subpath itself need not start at the root (see Figure 2.3). Give an algorithm for this problem that runs in time proportional to the total number of characters on the edges of the tree plus the length of P.

To be honest i am completely stuck and I can't think of an algorithm that can solve this. I guess we will use dynamic programming?

CodePudding user response：

Trincot has already answered this as a comment.

Use some known O(n m) search algorithms like Boyer-Moore's, and combine with a DFS traversal through the tree.

Adding my two cents to it.

How can we express this question in general terms? This basically is searching a pattern in a tree. So we need to build muscle on how to search for a pattern? and how to search in a tree?

1. Given a string, search for a pattern in the string.

If you solve with brute-force approach, you get time complexity of O(len(string) * len(pattern)). You can do this efficiently in O(len(string) len(pattern)) with known algorithms like

3. Now, if you can search over Binary tree, can you search over any kind of tree?

In your case, the label is on the edge. If the label was on a vertex, the tree would be called a Trie. Can you search in a Trie just like you did for 2(A) above? (Try 2(B) for exercise on Trie.)

If you can solve the above three, you'll have your answer. I was interested in showing you the thought process if you are new to this problem space. Anyways, you would get answers online to above three questions. Hope it helped!