Count all paths in a tree that have cost 0 modulo k-CodePudding

I have a tree, now I want to count the number of paths going up to the root of the tree, (it need not reach till root node).

While counting the paths, I want to find the cost for that path and do a calculation as (cost % k = 0), to find all such valid paths.

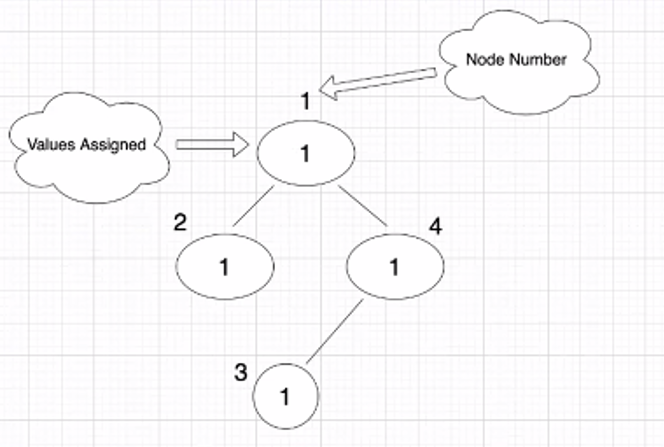
For input k = 2 and list = [1,1,1,1], from = [1,1,4], to = [2,4,3] List represent cost of every node. from and to represent the edges in the tree.

the tree represented as :

For the above tree, we have 8 possible paths:

1
2
4
2->1
4->1
3
3->4 (this has a path that can reach root node, so this path is considered)
3->4->1

But only valid paths are

2->1
4->1
3->4

that have cost % k = 0

so the result is 3.

This is my code, here I am checking from and to edges sum and checking if remainder with k is 0, also checking to edges with the remainder as 0.

public int findValidPaths(List<Integer> list, int nodes, List<Integer> from, List<Integer> to, int k) {
    int result = 0;
    for(int e : to) {
        if(list.get(e-1) % k == 0) {
            result  ;
        }
    }
    for(int i=0; i<from.size(); i  ) {
        int cost = list.get(from.get(i)-1)   list.get(to.get(i) -1);
        if(cost%k == 0) {
            result  ;
        }
    }
    return result   1;
}

My approach is not correct as I am not checking all paths, how to solve this problem.

constraints:

cost : 1 to 10^9 
k : 1 to 10^5

Another example:

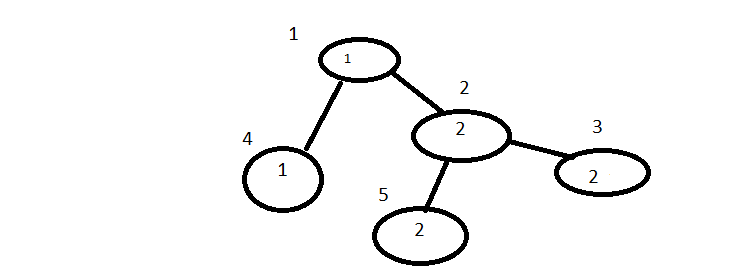
Inputs are : list = [1,2,2,1,2], from = [2,2,1,2], to = [3,1,4,5], k = 2

The expected output is 6 because valid combinations are:

4-1

CodePudding user response：

A general O(n) formulation can be let f(n) represent all the remainders that can be reached in prefix sums modulo k of traversals down from the root. Then node n can be paired with as many of those remainders that are the same as (sum_head n) % k, where sum_head is the prefix sum modulo k ending at ns parent.

In order to use space efficiently, we can use a map of sum mod k -> count, recursing down into the tree and unsetting the prefix sum we just created (i.e., backtracking) after the recursion.

For example, k = 3

            G(2)
        /          \
      E(1)         F(2)
     /    \       /   \
   A(2)  B(4)   C(2)  D(5)

Prefix sums modulo k = 3:

G -> E -> A
2    0    2
       -> B
          1

G -> F -> C
2    1    0
       -> D
          0

We arrive at E and count the 0 prefix sum there. At A, we match 2 with the 2 in the prefix_sum_mod_k map, which accounts for the path A -> E.

We backtrack, unsetting a 2 and examine B, which has no match in the map.

We backtrack to G, unsetting a 1 and a 0, and proceed to F, which has no match. We proceed to C, which is a 0 and count it. We backtrack to F, unsetting a 0, and proceed to D, counting one more 0.

Total: 4

E -> G
A -> E
C -> F -> G
D -> F -> G

Python code:

from collections import defaultdict

def f(k, costs, from_lst, to_lst):
  children = defaultdict(list)

  for i, u in enumerate(from_lst):
    children[u].append(to_lst[i])

  prefixes = defaultdict(int)
  prefixes[0] = 1

  def g(n, s):
    result = 0
    curr = (s   costs[n]) % k
    result  = prefixes[curr]
    prefixes[curr]  = 1
    for c in children[n]:
      result  = g(c, curr)
    prefixes[curr] -= 1
    return result

  return g(0, 0)

Output:

params = [
  (3, [2,1,2,2,4,2,5], [0,0,1,1,2,2], [1,2,3,4,5,6]),
  (2, [1,1,1,1], [0,0,3], [1,3,2]),
  (2, [1,2,2,1,2], [0,0,1,1], [1,3,2,4])
]

for args in params:
  print(f(*args), args)

"""
4 (3, [2, 1, 2, 2, 4, 2, 5], [0, 0, 1, 1, 2, 2], [1, 2, 3, 4, 5, 6])
3 (2, [1, 1, 1, 1], [0, 0, 3], [1, 3, 2])
6 (2, [1, 2, 2, 1, 2], [0, 0, 1, 1], [1, 3, 2, 4])
"""

CodePudding user response：

For code it is not clear which algorithm you are using for finding paths in tree but depth-first-search can be used to find paths in a graph or tree. https://www.geeksforgeeks.org/find-paths-given-source-destination/