Multiple types for f in this picture?-CodePudding

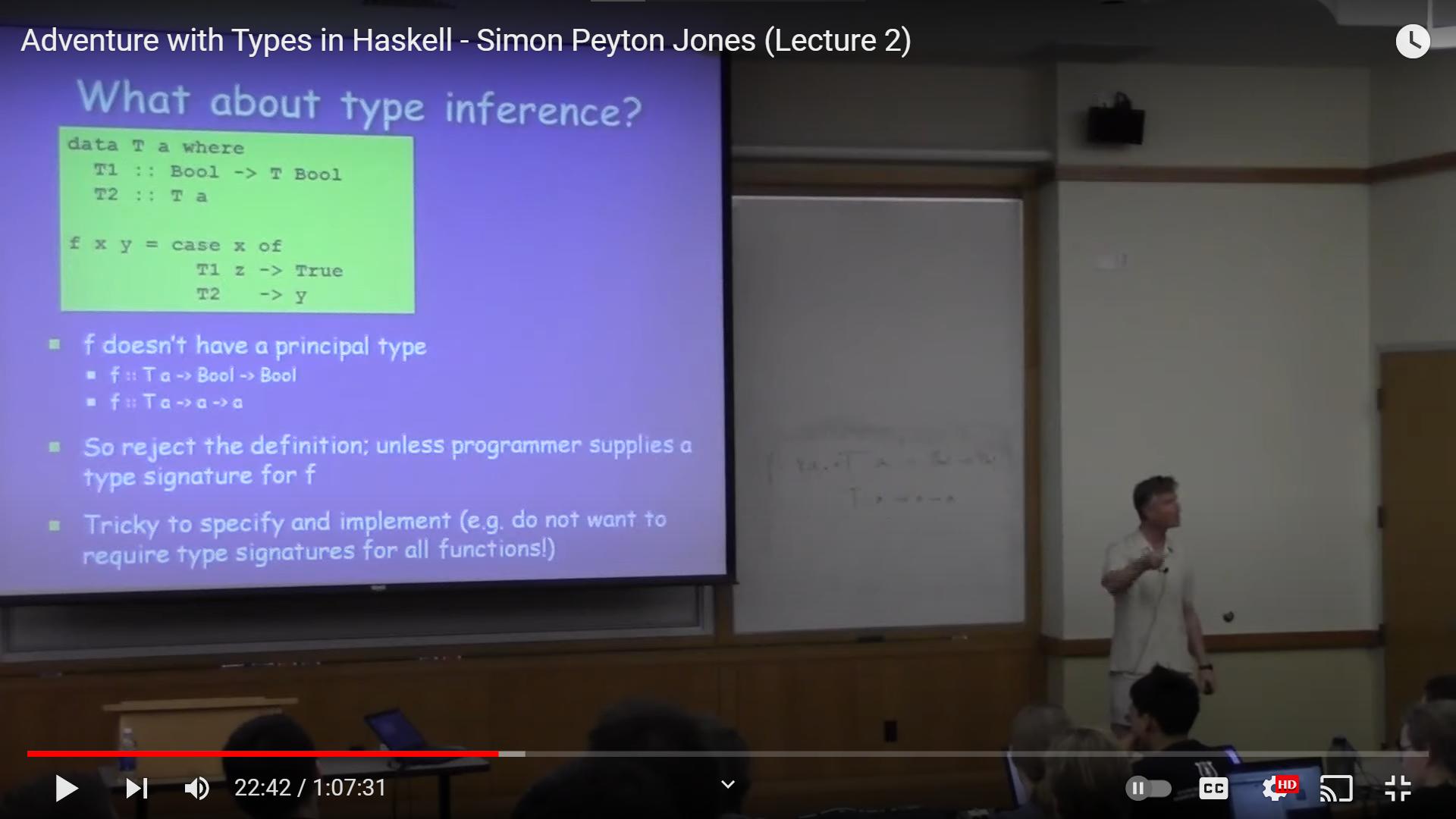
data T a where
  T1 :: Bool -> T Bool
  T2 :: T a

f x y = case x of
  T1 x -> True
  T2   -> y

Simon is saying that f could be typed as T a -> a -> a, but I would think the return value MUST be a Bool since that is an explicit result in a branch of the case expression. This is in regards to Haskell GADTs. Why is this the case?

CodePudding user response：

This is kind of the whole point of GADTs. Matching on a constructor can cause additional type information to come into scope.

Let's look at what happens when GHC checks the following definition:

f :: T a -> a -> a
f x y = case x of
    T1 _ -> True
    T2   -> y

Let's look at the T2 case first, just to get it out of the way. y and the result have the same type, and T2 is polymorphic, so you can declare its type is also T a. All good.

Then comes the trickier case. Note that I removed the binding of the name x inside the case as the shadowing might be confusing, the inner value isn't used, and it doesn't change anything in the explanation. When you match on a GADT constructor like T1, one that explicitly sets a type variable, it introduces additional constraints inside that branch which add that type information. In this case, matching on T1 introduces a (a ~ Bool) constraint. This type equality says that a and Bool match each other. Therefore the literal True with type Bool matches the a written in the type signature. y isn't used, so the branch is consistent with T a -> a -> a.

So it all matches up. T a -> a -> a is a valid type for that definition. But as Simon is saying, it's ambiguous. T a -> Bool -> Bool is also a valid type for that definition. Neither one is more general than the other, so the definition doesn't have a principle type. So the definition is rejected unless a type is provided, because inference cannot pick a single most-correct type for it.

CodePudding user response：

A value of type T a with a different from Bool can never have the form T1 x (since that has only type T Bool).

Hence, in such case, the T1 x branch in the case becomes inaccessible and can be ignored during type checking/inference.

More concretely: GADTs allow the type checker to assume type-level equations during pattern matching, and exploit such equations later on. When checking

f :: T a -> a -> a
f x y = case x of
  T1 x -> True
  T2   -> y

the type checker performs the following reasoning:

f :: T a -> a -> a
f x y = case x of
  T1 x -> -- assume: a ~ Bool
          True  -- has type Bool, hence it has also type a
  T2   -> -- assume: a~a  (pointless)
          y     -- has type a

Thanks to GADTs, both branches of the case have type a, hence the whole case expression has type a and the function definition type checks.

More generally, when x :: T A and the GADT constructor was defined as K :: ... -> T B then, when type checking we can make the following assumption:

case x of
  K ... ->  -- assume: A ~ B

Note that A and B can be types involving type variables (as in a~Bool above), so that allows one obtain useful information about them and exploit it later on.