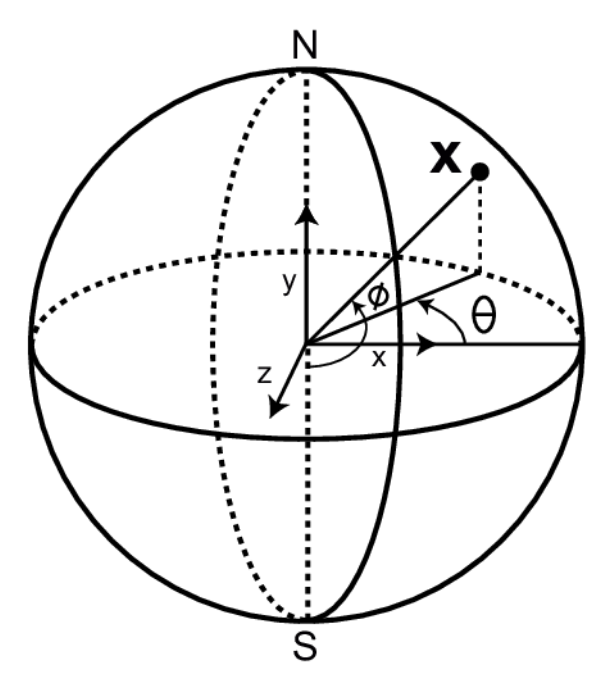
I've got a 3d sphere which I've been able to plot a point on using longitude and latitude thanks to some work of another developer I've found online. I think I understand what its doing.

What I need to do now is rotate my planet so the point is always at the top most point (ie the north pole) but I'm not sure how to do this. I'm probably missing some important fundamentals here so I'm hoping the answer can assist in my future learning.

Here's an image showing what I have - The blue line is a line coming from the longitude and latitude I have plotted and I need to rotate the planet so that line is basically pointing directly upwards.

Calculate the radius vector, which is just r = x-sphereCenter. Make a copy of it, set y to zero, so that you have (x, 0, z) - which is just the projection of the vector r on the horizontal xz-plane - let's call the copy rXZ.

Determine the signed angle between the x-axis and rXZ (use Vector3.SignedAngle(xAxis, rXZ, yAxis), see docs), and create a rotation matrix M1 that rotates the sphere in the opposite direction around the vertical (negate the angle). This should place your point in the xy-plane.

Now determine the angle between r and the y-axis (Vector3.SignedAngle(r, yAxis, zAxis)), and create a new rotation matrix M2 that rotates by that angle around the zAxis. (I think for this second one, the simpler Vector3.Angle will work as well.)

So, what you want now is to combine the two matrices (by multiplying them) into a single transform (I'm assuming this is a transformation in the local coordinate system of the sphere, where (0, 0, 0) is the sphere's center). If I'm not mistaken, Unity uses column-major matrices, so the multiplication order should be M = M2 * M1 (the rightmost matrix is applied first).

Reorient your globe using M as a local transform, and it should bring your point to the top. You can also create M3 = M1.inverse, and then do M = M3 * M2 * M1, to preserve the original angular offset from the xy-plane.

Check for edge cases, such as r already being vertical (pointing straight up, or straight down).