How can I determine which edges are part of simple paths between a vertex subset?-CodePudding

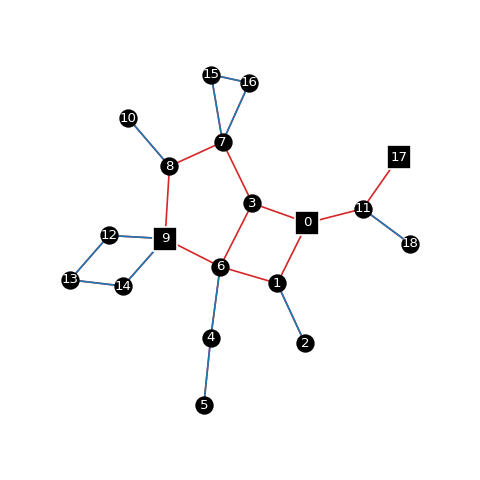
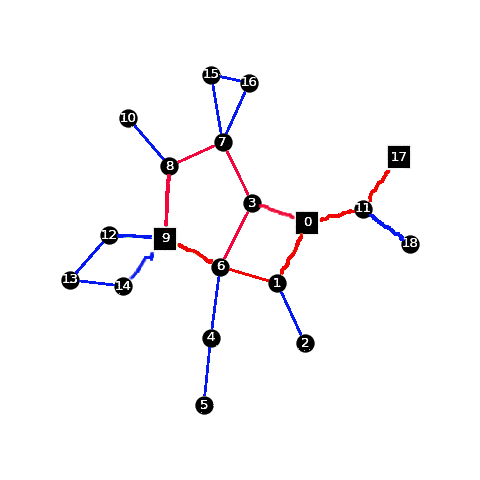
Problem:

I have an undirected graph (with cycles) given by a list of edges.
I'm given a list/subset of vertices/nodes (example: [0, 9, 17] below), which I refer to as "important vertices".
I want to color each edge based on whether it is part of some simple path [1] between the important vertices. In the example below, I have colored the edges red if they are part of such a simple path, and blue otherwise.

[1]: a simple path means any vertex can appear at most once in the path.

Does this problem have a name?
Are there any existing algorithms that solve this problem?
What is the optimal time comlexity? My gut feeling tells me it might be possible to solve this by visiting every edge a constant number of times. Once you know whether an edge is part of a simple path or not, you probably don't need to visit it again.

For every edge, perform a depth-first search in both directions to find out which important vertices are reachable through simple paths in both directions.
If either of the directions don't reach an important vertex, or only the single and same important vertex is reached in both directions, the edge will color itself blue - otherwise it will color itself red.
This almost works - but mistakenly colors the 15-16 edge red - and seems to scale really poorly, which is why I'm looking for a better way to do this.

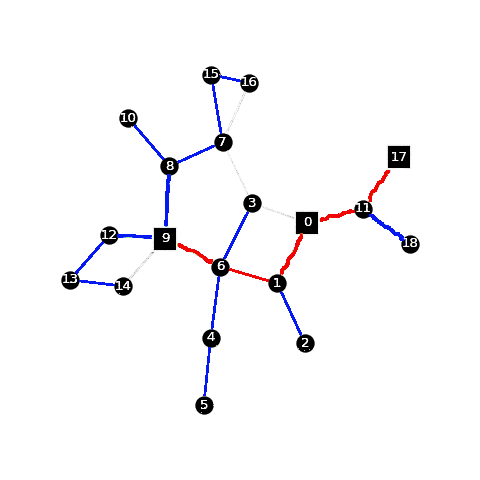
Any uncoloured edge forms a loop. If a loop has any edges that are red, re-colour it red, including the uncoloured edge. Go repeatedly through all the uncoloured edges until you cannot colour a loop red. Then, colour the remaining edges blue.

I think this works; because the red edges are necessarily connected.