Trying to simulate Poisson samples using inverse CDF method but my R function produces wrong results-CodePudding

I wrote some R code for simulating random samples from a Poisson distribution, based on the description of an algorithm (see attached image). But my code does not seem to work correctly, because the generated random samples are of a different pattern compared with those generated by R's built-in rpois() function. Can anybody tell me what I did wrong and how to fix my function?

r.poisson <- function(n, l=0.5)
{
  U <- runif(n)
  X <- rep(0,n)
  p=exp(-l)
  F=p
  for(i in 1:n)
  {
    if(U[i] < F)
    {
      X[i] <- i
    } else
    {
      p=p*l/(i 1)
      F=F p
      i=i 1
    }
  }
  return(X)
}

r.poisson(50)

The output is very different from rpois(50, lambda = 0.5). The algorithm I followed is:

algorithm

CodePudding user response：

(Thank you for your question. Now I know how a Poisson random variable is simulated.)

You had a misunderstanding. The inverse CDF method (with recursive computation) you referenced is used to generate a single Poisson random sample. So you need to fix this function to produce a single number. Here is the correct function, commented to help you follow each step.

rpois1 <- function (lambda) {
  ## step 1
  U <- runif(1)
  ## step 2
  i <- 0
  p <- exp(-lambda)
  F <- p
  ## you need an "infinite" loop
  ## no worry, it will "break" at some time
  repeat {
    ## step 3
    if (U < F) {
      X <- i
      break
    }
    ## step 4
    i <- i   1
    p <- lambda * p * i
    F <- F   p
    ## back to step 3
  }
  return(X)
}

Now to get n samples, you need to call this function n times. R has a nice function called replicate to repeat a function many times.

r.poisson <- function (n, lambda) {
  ## use `replicate()` to call `rpois1` n times
  replicate(n, rpois1(lambda))
}

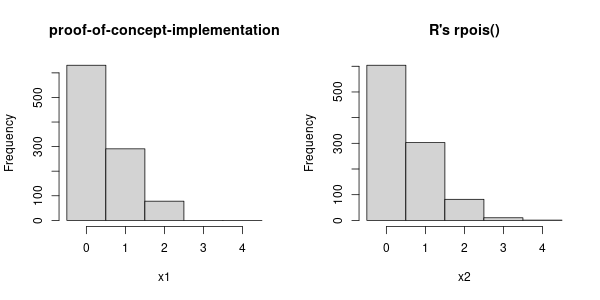
Now we can make a reasonable comparison with R's own rpois.

x1 <- r.poisson(1000, lambda = 0.5)
x2 <- rpois(1000, lambda = 0.5)

## set breaks reasonably when making a histogram
xmax <- max(x1, x2)   0.5
par(mfrow = c(1, 2))
hist(x1, main = "proof-of-concept-implementation", breaks = seq.int(-0.5, xmax))
hist(x2, main = "R's rpois()", breaks = seq.int(-0.5, xmax))

CodePudding user response：

A vectorized version will run much faster than a non-vectorized function using replicate. The idea is to iteratively drop the uniform random samples as i is incremented.

r.poisson1 <- function(n, l = 0.5) {
  U <- runif(n)
  i <- 0L
  X <- integer(n)
  p <- exp(-l)
  F <- p
  idx <- 1:n
  while (length(idx)) {
    bln <- U < F
    X[idx[bln]] <- i
    p <- l*p/(i <- i   1L)
    F <- F   p
    idx <- idx[!bln]
    U <- U[!bln]
  }
  X
}

@Zheyuan Li's non-vectorized functions:

rpois1 <- function (lambda) {
  ## step 1
  U <- runif(1)
  ## step 2
  i <- 0
  p <- exp(-lambda)
  F <- p
  ## you need an "infinite" loop
  ## no worry, it will "break" at some time
  repeat {
    ## step 3
    if (U < F) {
      X <- i
      break
    }
    ## step 4
    i <- i   1
    p <- lambda * p * i
    F <- F   p
    ## back to step 3
  }
  return(X)
}

r.poisson2 <- function (n, lambda) {
  ## use `replicate()` to call `rpois1` n times
  replicate(n, rpois1(lambda))
}

Benchmark:

microbenchmark::microbenchmark(r.poisson1(1e5),
                               r.poisson2(1e5, 0.5),
                               rpois(1e5, 0.5))
#> Unit: milliseconds
#>                    expr        min         lq       mean     median         uq        max neval
#>       r.poisson1(1e 05)   3.063202   3.129151   3.782200   3.225402   3.734600  18.377700   100
#>  r.poisson2(1e 05, 0.5) 217.631002 244.816601 269.692648 267.977001 287.599251 375.910601   100
#>       rpois(1e 05, 0.5)   1.519901   1.552300   1.649026   1.579551   1.620451   7.531401   100