I'm implementing a function in c which takes a double as a parameter and returns a arsinh value of that double. I'm using a lookup table for my implementation to approximate my results and currently I have an error of ±0.005 and cover the ranges from -1000000 to 1000000 approximately. The problem I have now is that this function needs to cover the entire range of a double but I don't know how this can be done since the max value of a double is 1.7976931348623157E 308. Would there be some other way to approximate arsinh for extremely big values?
#include <stddef.h>
#include <stdlib.h>
#include <emmintrin.h>
#include <stdint.h>
#include <stdbool.h>
double hashMap(double x) {
typedef struct {
int k;
double v;
} map;
map items[] = {
//increment 0.2
{0, 0.0}, {1, 0.198690110349}, {2, 0.390035319771}, {3, 0.568824898732}, {4, 0.732668256045}, {5, 0.88137358702},
{6, 1.01597313418}, {7, 1.13798204629}, {8, 1.2489833279}, {9, 1.35044074027}, {10, 1.44363547518},
{11, 1.52966049509}, {12, 1.60943791243}, {13, 1.683743144}, {14, 1.75322890111},
//increment 0.5 start: 3
{15, 1.81844645923},
{16, 1.96572047165}, {17, 2.09471254726},
{18, 2.20934770862}, {19, 2.31243834127},
{20, 2.4060591253}, {21, 2.49177985264},
{22, 2.5708146781}, {23, 2.64412076106},
{24, 2.71246530518},
//increment 2 start: 8
{25, 2.77647228072},
{26, 2.9982229503},
{27, 3.1797854377},
{28, 3.33347758688},
{29, 3.46671103788},
{30, 3.58428965186},
//increment 4 start: 20
{31, 3.68950386899},
{32, 3.87163475639},
{33, 4.02567041587},
{34, 4.15912713463},
{35, 4.27685896446},
{36, 4.38218284807},
{37, 4.4774659217},
{38, 4.56445668076},
{39, 4.64448334194},
{40, 4.71857858115},
//increment 10 start: 60
{41, 4.78756117999},
{42, 4.94169343911},
//increment 20 start: 80
{43, 5.07521287545},
{44, 5.29834236561},
{45, 5.480656284},
{46, 5.63480235803},
{47, 5.76833076128},
{48, 5.88611174741},
{49, 5.99147079705},
//increment 50 start: 200
{50, 5.99147079705},
{51, 6.2146120984},
{52, 6.39693243298},
{53, 6.55108237585},
{54, 6.68461329016},
{55, 6.80239599789},
//increment 100 start: 500
{56, 6.90775627898},
{57, 7.09007753022},
{56, 7.24422802581},
{57, 7.37775929885},
{56, 7.49554225253},
//increment 200 start: 1000
{57, 7.60090270954},
{58, 7.78322418995},
{59, 7.93737482371},
{60, 8.07090618644},
{61, 8.1886892016},
{62, 8.2940497026},
{63, 8.1886892016},
{64, 7.49554225253},
{65, 8.55641394155},
{66, 8.63052190861},
//increment 1000 start: 3000
{67, 8.69951477599},
{68, 8.98719683629},
{69, 9.21034038198},
{70, 9.39266193571},
{71, 9.5468126137},
{72, 9.68034400513},
{73, 9.79812703996},
//increment 2000 start: 10000
{74, 9.90348755504},
{75, 10.0858091111},
{76, 10.2399597904},
{77, 9.90348755504},
//increment 5000 start: 20000
{78, 10.5966347337},
{79, 10.8197782848},
{80, 11.0020998415},
{81, 11.1562505212},
{82, 11.2897819138},
{83, 11.4075649494},
//increment 15000 start: 50000
{84, 11.5129254651},
{85, 11.7752897295},
{86, 11.9829290943},
{87, 12.1547793512},
//increment 20000 start: 110000
{88, 12.3013828254},
{89, 12.46843691},
{90, 12.6115377536},
{91, 12.7367008966},
{92, 12.8479265317},
// increment 40000 start: 210000
{93, 12.9480099903},
// increment 50000 start: 250000
{94, 13.1223633774},
// increment 100000 start: 300000
{95, 13.3046849342},
{96, 13.5923670067},
// increment 200000 start: 500000
{97, 13.815510558},
{98, 14.1519827946},
{99, 14.4032972229},
};
double m = 0;
double c = 0;
if (x <= 0.2) {
m = items[1].v / 0.2;
c = items[1].v - m * 0.2;
} else if (x <= 0.4) {
m = (items[2].v - items[1].v) / 0.2;
c = items[1].v - m * 0.2;
} else if (x <= 0.6) {
m = (items[3].v - items[2].v) / 0.2;
c = items[2].v - m * 0.4;
} else if (x <= 0.8) {
m = (items[4].v - items[3].v) / 0.2;
c = items[3].v - m * 0.6;
} else if (x <= 1.0) {
m = (items[5].v - items[4].v) / 0.2;
c = items[4].v - m * 0.8;
} else if (x <= 1.2) {
m = (items[6].v - items[5].v) / 0.2;
c = items[5].v - m * 1.0;
} else if (x <= 1.4) {
m = (items[7].v - items[6].v) / 0.2;
c = items[6].v - m * 1.2;
} else if (x <= 1.6) {
m = (items[8].v - items[7].v) / 0.2;
c = items[7].v - m * 1.4;
} else if (x <= 1.8) {
m = (items[9].v - items[8].v) / 0.2;
c = items[8].v - m * 1.6;
} else if (x <= 2.0) {
m = (items[10].v - items[9].v) / 0.2;
c = items[9].v - m * 1.8;
} else if (x <= 2.2) {
m = (items[11].v - items[10].v) / 0.2;
c = items[10].v - m * 2.0;
} else if (x <= 2.4) {
m = (items[12].v - items[11].v) / 0.2;
c = items[11].v - m * 2.2;
} else if (x <= 2.6) {
m = (items[13].v - items[12].v) / 0.2;
c = items[12].v - m * 2.4;
} else if (x <= 2.8) {
m = (items[14].v - items[13].v) / 0.2;
c = items[13].v - m * 2.6;
} else if (x <= 3.0) {
m = (items[15].v - items[14].v) / 0.2;
c = items[14].v - m * 2.8;
} else if (x <= 3.5) {
m = (items[16].v - items[15].v) / 0.5;
c = items[15].v - m * 3.0;
} else if (x <= 4.0) {
m = (items[17].v - items[16].v) / 0.5;
c = items[16].v - m * 3.5;
} else if (x <= 4.5) {
m = (items[18].v - items[17].v) / 0.5;
c = items[17].v - m * 4.0;
} else if (x <= 5.0) {
m = (items[19].v - items[18].v) / 0.5;
c = items[18].v - m * 4.5;
} else if (x <= 5.5) {
m = (items[20].v - items[19].v) / 0.5;
c = items[19].v - m * 5.0;
} else if (x <= 6.0) {
m = (items[21].v - items[20].v) / 0.5;
c = items[20].v - m * 5.5;
} else if (x <= 6.5) {
m = (items[22].v - items[21].v) / 0.5;
c = items[21].v - m * 6.0;
} else if (x <= 7.0) {
m = (items[23].v - items[22].v) / 0.5;
c = items[22].v - m * 6.5;
} else if (x <= 7.5) {
m = (items[24].v - items[23].v) / 0.5;
c = items[23].v - m * 7.0;
} else if (x <= 8) {
m = (items[25].v - items[24].v) / 0.5;
c = items[24].v - m * 7.5;
} else if (x <= 10) {
m = (items[26].v - items[25].v) / 2;
c = items[25].v - m * 8.0;
} else if (x <= 12) {
m = (items[27].v - items[26].v) / 2;
c = items[26].v - m * 10.0;
} else if (x <= 14) {
m = (items[28].v - items[27].v) / 2;
c = items[27].v - m * 12.0;
} else if (x <= 16) {
m = (items[29].v - items[28].v) / 2;
c = items[28].v - m * 14.0;
} else if (x <= 18) {
m = (items[30].v - items[29].v) / 2;
c = items[29].v - m * 16.0;
} else if (x <= 20) {
m = (items[31].v - items[30].v) / 2;
c = items[30].v - m * 18.0;
} else if (x <= 24) {
m = (items[32].v - items[31].v) / 4;
c = items[31].v - m * 20.0;
} else if (x <= 28) {
m = (items[33].v - items[32].v) / 4;
c = items[32].v - m * 24.0;
} else if (x <= 32) {
m = (items[34].v - items[33].v) / 4;
c = items[33].v - m * 28.0;
} else if (x <= 36) {
m = (items[35].v - items[34].v) / 4;
c = items[34].v - m * 32.0;
} else if (x <= 40) {
m = (items[36].v - items[35].v) / 4;
c = items[35].v - m * 36.0;
} else if (x <= 44) {
m = (items[37].v - items[36].v) / 4;
c = items[36].v - m * 40.0;
} else if (x <= 48) {
m = (items[38].v - items[37].v) / 4;
c = items[37].v - m * 44.0;
} else if (x <= 52) {
m = (items[39].v - items[38].v) / 4;
c = items[38].v - m * 48.0;
} else if (x <= 56) {
m = (items[40].v - items[39].v) / 4;
c = items[39].v - m * 52.0;
} else if (x <= 60) {
m = (items[41].v - items[40].v) / 4;
c = items[40].v - m * 56.0;
} else if (x <= 70) {
m = (items[42].v - items[41].v) / 10;
c = items[41].v - m * 60.0;
} else if (x <= 80) {
m = (items[43].v - items[42].v) / 10;
c = items[42].v - m * 70.0;
} else if (x <= 100) {
m = (items[44].v - items[43].v) / 20;
c = items[43].v - m * 80;
} else if (x <= 120) {
m = (items[45].v - items[44].v) / 20;
c = items[44].v - m * 100;
} else if (x <= 140) {
m = (items[46].v - items[45].v) / 20;
c = items[45].v - m * 120;
} else if (x <= 160) {
m = (items[47].v - items[46].v) / 20;
c = items[46].v - m * 140;
} else if (x <= 180) {
m = (items[48].v - items[47].v) / 20;
c = items[47].v - m * 160;
} else if (x <= 200) {
m = (items[49].v - items[48].v) / 20;
c = items[48].v - m * 180;
} else if (x <= 250) {
m = (items[50].v - items[49].v) / 50;
c = items[49].v - m * 200;
} else if (x <= 300) {
m = (items[51].v - items[50].v) / 50;
c = items[50].v - m * 250;
} else if (x <= 350) {
m = (items[52].v - items[51].v) / 50;
c = items[51].v - m * 300;
} else if (x <= 400) {
m = (items[53].v - items[52].v) / 50;
c = items[52].v - m * 350;
} else if (x <= 450) {
m = (items[54].v - items[53].v) / 50;
c = items[53].v - m * 400;
} else if (x <= 500) {
m = (items[55].v - items[54].v) / 50;
c = items[54].v - m * 450;
} else if (x <= 600) {
m = (items[56].v - items[55].v) / 100;
c = items[55].v - m * 500;
} else if (x <= 700) {
m = (items[57].v - items[56].v) / 100;
c = items[56].v - m * 600;
} else if (x <= 800) {
m = (items[58].v - items[57].v) / 100;
c = items[57].v - m * 700;
} else if (x <= 900) {
m = (items[59].v - items[58].v) / 100;
c = items[58].v - m * 800;
} else if (x <= 1000) {
m = (items[60].v - items[59].v) / 100;
c = items[59].v - m * 900;
} else if (x <= 1200) {
m = (items[61].v - items[60].v) / 200;
c = items[60].v - m * 1000;
} else if (x <= 1400) {
m = (items[62].v - items[61].v) / 200;
c = items[61].v - m * 1200;
} else if (x <= 1600) {
m = (items[63].v - items[62].v) / 200;
c = items[62].v - m * 1400;
} else if (x <= 1800) {
m = (items[64].v - items[63].v) / 200;
c = items[63].v - m * 1600;
} else if (x <= 2000) {
m = (items[65].v - items[64].v) / 200;
c = items[64].v - m * 1800;
} else if (x <= 2200) {
m = (items[66].v - items[65].v) / 200;
c = items[65].v - m * 2000;
} else if (x <= 2400) {
m = (items[67].v - items[66].v) / 200;
c = items[66].v - m * 2200;
} else if (x <= 2600) {
m = (items[68].v - items[67].v) / 200;
c = items[67].v - m * 2400;
} else if (x <= 2800) {
m = (items[69].v - items[68].v) / 200;
c = items[68].v - m * 2600;
} else if (x <= 3000) {
m = (items[70].v - items[69].v) / 200;
c = items[69].v - m * 2800;
}
return m*x c;
}
double approxArsinh_lookup(double x) {
bool neg = false;
if (x < 0) {
x = abs(x);
neg = true;
}
if (neg) return -hashMap(x);
return hashMap(x);
}
int main() {
printf("%f\n", approxArsinh_lookup(0));
return 0;
}
CodePudding user response:
As here is the graph of arsinh function.
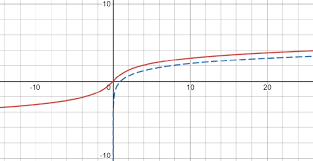
From the graph, it is possible to assume that when input greater than a value we could use the external approximate approach (use the m, c of the last element) to calculate for really large value without impact to the accuracy. If you want to have better accuracy, you could try to find the max value which provide enough accuracy for you.
For me, I will make the table a little different to make the code shorter. Assume change the struct a little bit:
typedef struct {
double min;
double v;
} map;
Then in the implementation, you could do loop as below:
double m = 0;
double c = 0;
int i;
for (i = 1; i < MAX_ARRAY_SIZE; i ;) // skip the first value which is 0
{
if ((x < items[i].min) && ( x > items[i-1].min))
{
m = (items[i].v - items[i-1].v) / (items[i].min - items[i-1].min);
c = items[i].v - m * items[i].min;
break;
}
}
if (i == MAX_ARRAY_SIZE) // input value is greater than array size
{
m = (items[MAX_ARRAY_SIZE - 1].v - items[MAX_ARRAY_SIZE - 2].v) / (items[MAX_ARRAY_SIZE - 1].min - items[MAX_ARRAY_SIZE - 2].min);
c = items[MAX_ARRAY_SIZE - 1].v - m * items[MAX_ARRAY_SIZE - 1].min;
}
