get time for a given probability in logistic regression

With this data set and logistic regression model:

dat1 <- data.frame(time=rep(seq(1,10), times=3), response=c(0,0,0,1,0,1,1,1,1,1, 0,0,0,0,0,1,1,1,1,1, 0,1,0,0,0,0,1,1,1,1), run=rep(c(1,2,3), each=10))

mod <- glm(response ~ time, data=dat1, family="binomial")

How can I extract what time will be given a certain probability? For example, how to get time for a probability of 0.5?

CodePudding user response：

Such "find x given y" problem is a root-finding problem.

You question is somehow special. The GLM response ~ time implies that the logistic curve in this case is a monotonic function of time. So for any target probability, there is only one root. This makes it trivial to apply any numerical method to find this root. Let's just use uniroot, which is very verbose.

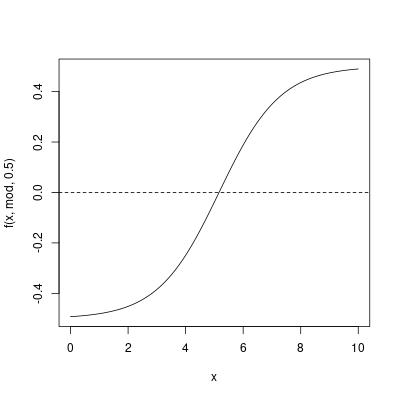
## we want to find the root of this function
## i.e., where it crosses 0
f <- function (tm, model, prob.target) {
  predict(model, newdata = data.frame(time = tm), type = "response") - prob.target
}

## try different lower bound 'lwr' and upper bound 'upr'
## until you see that the curve crosses the horizontal line at 0
lwr <- 0
upr <- 10
curve(f(x, mod, 0.5), lwr, upr)
abline(h = 0, lty = 2)

## use this 'lwr' and 'upr' for uniroot()
uniroot(f, c(lwr, upr), model = mod, prob.target = 0.5)$root
#[1] 5.160737

I see. I asked the question because @FP0 calculated the time as 4.68/0.94 = 5.16 in this answer, so I thought maybe there is a simple relationship that I'm missing.

Because the analytical expression of this GLM is known:

log(p / (1 - p)) = intercept slope * time

When p = 0.5, the left hand side is 0. So the root is simply:

time = -(intercept / slope)

The R code is:

unname(-(mod$coef[1] / mod$coef[2]))
#[1] 5.160737

So, I showed how to do this both analytically and numerically. I prioritized numerical one because Stack Overflow is a coding website :D