How to find the distance between a point x,y and the diagonales?-CodePudding

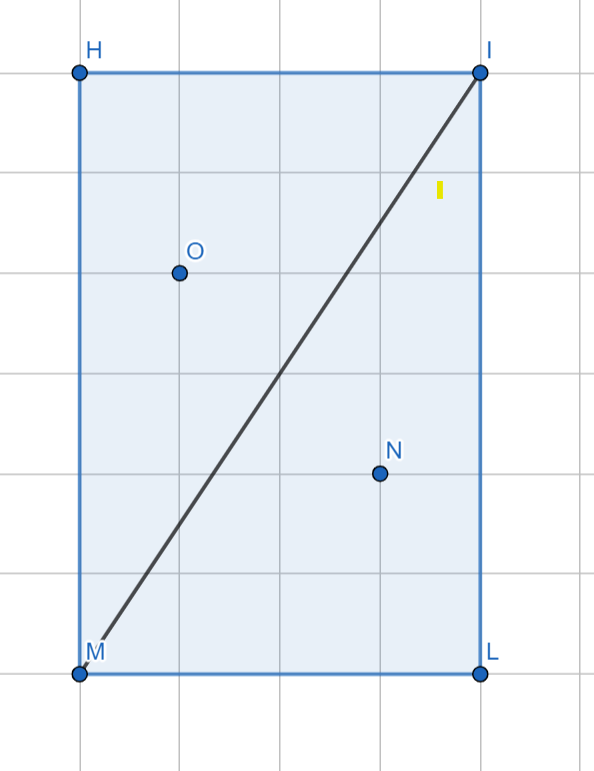
I need to find the distance of O and N with the diagonales (with a 90° angle/ the shortest). I found a formula online, but why in this case, it does not return the good distance ? And if possible, how to normalize the result (e.g. O is at20% of the diagonale?)

import numpy as np
import math

O = (1,3)
N = (3,2)

r = np.arange(24).reshape((6, 4))

def get_diagonal_distance(centroid, img_test):
 
   x1, y1 = centroid
   a, b  = img.shape[1], img.shape[0]
   c = np.sqrt(np.square(a)   np.square(b))
   d = abs((a * x1   b * y1   c)) / (math.sqrt(a * a   b * b))
   return d

   print(f"diagonal d: {get_diagonal_distance(O, r): .4f}")

CodePudding user response：

 d = abs((a * x1   b * y1   c)) / (math.sqrt(a * a   b * b))

Your computation is wrong because a, b and c refer to the coefficients of the equation of the line ax by c=0

import numpy as np

O = (1,3)
N = (3,2)


M, L, I, H = (-1,-2), (3, -2), (3, 2), (-1, 2)

# Following your initial idea
def get_diagonal_distance(diagonal_extremes, point):
    diagonal_vector = (diagonal_extremes[1][0] - diagonal_extremes[0][0],
                        diagonal_extremes[1][1] - diagonal_extremes[0][1])

    a = diagonal_vector[1]
    b = - diagonal_vector[0]
    c = - diagonal_extremes[0][0]*a - diagonal_extremes[0][1]*b
    x, y = point[0], point[1]

    return abs((a * x   b * y   c)) / (np.sqrt(a * a   b * b))

# Taking advantage of numpy
def distance_from_diagonal(diagonal_extremes, point):
    u = (diagonal_extremes[1][0] - diagonal_extremes[0][0],
            diagonal_extremes[1][1] - diagonal_extremes[0][1])
    v = (point[0] - diagonal_extremes[0][0],
        point[1] - diagonal_extremes[0][1])
    return np.cross(u, v) / np.linalg.norm(u)

print(f"diagonal d: {get_diagonal_distance((M, I), O): .4f}")
print(f"diagonal d: {distance_from_diagonal((M, I), O): .4f}")